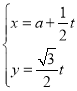题目内容
【题目】如图，平面
平面
，四边形
和
都是边长为2的正方形，点
，
分别是
，
的中点，二面角
的大小为60°.
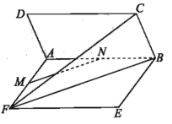
（1）求证：
平面
；
（2）求三棱锥
的体积.
【答案】（1）证明见解析；（2）
.
【解析】
（1）由中位线性质可知
，又
平面
，
平面即可求证；
（2）根据题目条件不难得出
就是二面角
的平面角，连接
，解三角形可得
为直角三角形，由
进一步求证可得
平面
,又
平面，可得点
到平面的距离等于点
到平面的距离，即为所求三棱锥的高，再求出底面积代入体积公式即可.
（1）证明：
，
分别是
，
的中点，
.
平面，平面，
平面.
（2）
四边形
和都是边长为2的正方形，
，
，
就是二面角的平面角，
.
连接，在中，
，
，
，
，
.
，
.
，，
，
平面
，
.
平面.
平面，
点到平面的距离等于点到平面的距离，为
.
，为的中点，
，
平面，
.
.
练习册系列答案
相关题目
