题目内容
4.非空集合A={x|1≤x≤a},B={y|y=x+1,x∈A},C={y|y=x2,x∈A},若B∩C≠∅,则a的取值范围为a≥$\sqrt{2}$.分析 根据A,以及B、C与A的关系表示出B与C,由B与C的交集不为空集确定出a的范围即可.
解答 解:∵非空集合A={x|1≤x≤a},B={y|y=x+1,x∈A},C={y|y=x2,x∈A},
∴B={y|2≤y≤a+1},C={y|1≤y≤a2},
∵B∩C≠∅,
∴a2≥2且a+1≥2,
解得:a≥$\sqrt{2}$或a≤-$\sqrt{2}$,且a≥1,
则a的范围为a≥$\sqrt{2}$,
故答案为:a≥$\sqrt{2}$
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

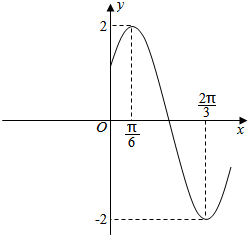 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.