题目内容
3. 已知多面体ABDEC中,底面△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,且EC,DB在平面ABC的同侧,M为EA的中点,CE=CA=2DB=2
已知多面体ABDEC中,底面△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,且EC,DB在平面ABC的同侧,M为EA的中点,CE=CA=2DB=2(Ⅰ)求证:DM∥平面ABC;
(Ⅱ)求证:平面DEA⊥平面ECA;
(Ⅲ)求此多面体ABDEC的体积.
分析 (Ⅰ)取AC的中点N,连接MN,BN,利用三角形中位线定理与平行四边形的判定与性质定理可得DM∥BN,再利用线面平行的判定定理可得:DM∥平面ABC.
(Ⅱ)由EC⊥平面ABC,可得EC⊥BN,利用△ABC为正三角形,可得BN⊥AC,可得BN⊥平面ECA,利用DM∥BN,可得DM⊥平面ECA,即可证明.
(Ⅲ)取BC的中点O,连接AO,利用等边三角形的性质可得:AO⊥BC.利用面面垂直的性质定理可得:AO⊥平面BDEC.利用此多面体ABDEC的体积V=VA-BDEC=$\frac{1}{3}h{S}_{BDEC}$即可得出.
解答 (Ⅰ)证明:取AC的中点N,连接MN,BN,
∵$MN\underset{∥}{=}\frac{1}{2}EC$,$DB\underset{∥}{=}\frac{1}{2}EC$,
∴$MN\underset{∥}{=}$DB,
故四边形BDMN为平行四边形,
由DM∥BN,DM?平面ABC,BN?平面ABC,
∴DM∥平面ABC.
(Ⅱ)证明:∵EC⊥平面ABC,BN?平面ABC,
∴EC⊥BN,
又∵△ABC为正三角形,
N为AC的中点,
∴BN⊥AC,
又AC∩EC=C,
∴BN⊥平面ECA,
∵DM∥BN,
∴DM⊥平面ECA,
又DM?平面DEA,
∴平面DEA⊥平面ECA.
(Ⅲ)解:取BC的中点O,连接AO,
∵△ABC是边长为2的等边三角形,
∴AO⊥BC,AO=$\sqrt{3}$.
∵平面BDEC⊥平面ABC,平面BDEC∩平面ABC=BC,
∴AO⊥平面BDEC.
SBDEC=$\frac{(1+2)×2}{2}$=3,
∴此多面体ABDEC的体积V=VA-BDEC=$\frac{1}{3}h{S}_{BDEC}$=$\frac{1}{3}×\sqrt{3}×3$=$\sqrt{3}$.
点评 本题考查了线面面面平行与垂直的判定性质定理、三角形的中位线定理、四棱锥的体积计算公式、平行四边形的判定与性质定理,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案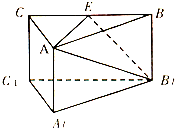 如图,三棱柱中,侧棱AA1⊥底面A1B1C1,三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱中,侧棱AA1⊥底面A1B1C1,三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | A1C1⊥平面ABB1A1 | ||
| C. | AE,B1C1为异面直线,且AE⊥B1C1 | D. | A1C1∥平面A1EB |
 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5. 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.