题目内容
15.角α顶点在坐标顶点O,始边与x轴正半轴重合,终边与单位圆交于A(-$\frac{3}{5}$,$\frac{4}{5}$),将α终边绕O顺时针旋转$\frac{π}{3}$后,与单位圆交于B,则B横坐标$\frac{-3+4\sqrt{3}}{10}$.分析 利用三角函数的定义,结合差角的余弦公式,即可求出B横坐标.
解答 解:由题意,cosα=-$\frac{3}{5}$,sinα=$\frac{4}{5}$,
∴cos(α-$\frac{π}{3}$)=(-$\frac{3}{5}$)×$\frac{1}{2}$+$\frac{4}{5}$×$\frac{\sqrt{3}}{2}$=$\frac{-3+4\sqrt{3}}{10}$,
∴B横坐标为$\frac{-3+4\sqrt{3}}{10}$.
故答案为:$\frac{-3+4\sqrt{3}}{10}$.
点评 本题考查三角函数的定义,差角的余弦公式,考查学生的计算能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
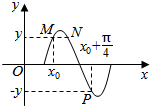 若函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示.
若函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示.