题目内容

已知锐角△ABC中，a、b、c分别为角A、B、C所对的边，且2sin(c+
π
3
)=sin2C+sin
π
3
．
（1）求角C的大小；
（2）若a=4，设D是BC的中点，
AD
•
AC
=2
AB
•
AC
，求△ABC的面积．
分析：（1）根据两角和的正弦公式和二倍角三角函数公式，将已知等式化简整理得：sinC+
3
cosC=2sinCcosC+
3
2
，再因此分解得（2cosC-1）（
3
2
-sinC）=0，最后结合△ABC是锐角三角形，可得出C=
π
3
；
（2）D是BC的中点，得
AD
=
1
2
（
AB
+
AC
），代入
AD
•
AC
=2
AB
•
AC
并化简整理，得2
AC
2=3
BC
•
AC
=
3
2
|
BC
|•|
AC
|，
因此，|
AC
|=
3
4
|
BC
|即b=
3
4
a=3，再由正弦定理的面积公式，即可算出△ABC的面积．
解答：解：（1）∵2sin(c+
π
3
)=sin2C+sin
π
3

∴2（sinCcos
π
3
+cosCsin
π
3
）=2sinCcosC+
3
2

即sinC+
3
cosC=2sinCcosC+
3
2
，移项整理得：（2cosC-1）（
3
2
-sinC）=0
∴cosC=
1
2
或sinC=
3
2
，结合C为锐角，可得C=
π
3

（2）∵D是BC的中点，得
AD
=
1
2
（
AB
+
AC
）
∴
AD
•
AC
=2
AB
•
AC
即
1
2
（
AB
+
AC
）•
AC
=2
AB
•
AC

化简整理，得
AC
2=3
AB
•
AC
=3（
AC
+
CB
）•
AC

∴2
AC
2=3
BC
•
AC
=3|
BC
|•|
AC
|cosC=
3
2
|
BC
|•|
AC
|
因此，|
AC
|=
3
4
|
BC
|即b=
3
4
a=3
∴△ABC的面积S=
1
2
absinC=
1
2
×4×3×sinC=3
3
．
点评：本题给出锐角三角形，在已知三角等式的情况下求角C的大小，求三角形的面积，着重考查了两角和的正弦公式、正弦定理和向量数量积的运算公式等知识，属于中档题．
练习册系列答案
相关题目
已知锐角△ABC中，角A、B、C的对边分别为a，b，c，a=
2
，b=
3
，B=
π
3
．
（Ⅰ）求角A的大小；
（Ⅱ）设函数f(x)=cosB•sin2x+cos2x，当x∈[-
π
4
，0]时，求f（x）的值域．
已知锐角△ABC中的三个内角分别为A，B，C．
（1）设
BC
•
CA
=
CA
•
AB
，求证：△ABC是等腰三角形；
（2）设向量
s
=（2sinC，-
3
），
t
=（cos2C，2cos2
C
2
-1），且
s
∥
t
，若sinA=
2
3
，求sin（
π
3
-B）的值．
（2009•淮安模拟）已知锐角△ABC中内角A，B，C的对边分别为a，b，c，且c=6，向量
s
=（2sinC，-
3
），
t
=（cos2C，2cos2
C
2
-1），且
s
∥
t
．
（1）求C的大小；
（2）若sinA=
1
3
，求sin(
π
3
-B)的值．
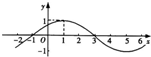已知函数f（x）=Asin（ωx+φ）（其中x∈R，A?＞0，ω＞0，-
π
2
＜φ＜
π
2
）的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）已知锐角△ABC中的三个内角分别为A，B，C，若有f（
A
π
）=
3
2
，边BC=
7
，sin B=
21
7
求△ABC的面积．
已知锐角△ABC中，三个内角为A，B，C，两向量
p
=（2-2sinA，cosA+sinA），
q
=（sinA-cosA，1+sinA），若
p
与
q
是共线向量．
（1）求∠A的大小；  
（2）求函数y=2sin2B+cos(
C-3B
2
)取最大值时，∠B的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网