题目内容
 选修4-1:几何证明选讲
选修4-1:几何证明选讲如图所示,AB为⊙O的直径,BC、CD为⊙O的切线,B、D为切点
(1)求证:AD∥OC
(2)若⊙O的半径为1,求AD•OC的值.
分析:(1)如图,连接BD、OD,BD交OC于M.由切线的性质证出BD⊥OC,得∠ODM+∠DOC=90°,而AB为⊙O直径,得∠ADO+∠ODM=90°,可得∠ADO=∠DOC,从而得出AD∥OC;
(2)根据题意,利用相似三角形判定定理证出Rt△BAD∽Rt△COD,从而得出AD•OC=AB•OD=2×1=2.
(2)根据题意,利用相似三角形判定定理证出Rt△BAD∽Rt△COD,从而得出AD•OC=AB•OD=2×1=2.
解答:解:(1)如图,连接BD、OD,BD交OC于M.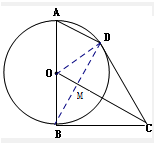
∵CB、CD是⊙O的两条切线,
∴BD⊥OC,
∴∠ODM+∠DOC=90°
又∵AB为⊙O直径,得AD⊥DB,
∴∠ADO+∠ODM=90°,可得∠ADO=∠DOC,
∴AD∥OC
(2)∵AO=OD,∴∠ADO=∠A=∠DOC,
由此可得Rt△BAD∽Rt△COD,
∴
=
,得AD•OC=AB•OD=2×1=2,
即AD•OC的值为2.

∵CB、CD是⊙O的两条切线,
∴BD⊥OC,
∴∠ODM+∠DOC=90°
又∵AB为⊙O直径,得AD⊥DB,
∴∠ADO+∠ODM=90°,可得∠ADO=∠DOC,
∴AD∥OC
(2)∵AO=OD,∴∠ADO=∠A=∠DOC,
由此可得Rt△BAD∽Rt△COD,
∴
| AB |
| CO |
| AD |
| OD |
即AD•OC的值为2.
点评:本题给出圆的两条切线和一条直径,求证直线平行并求线段的乘积.着重考查了圆的切线的性质、三角形相似的判定与性质等知识,属于中档题.

练习册系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲