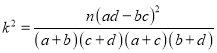[题目]选修44:坐标系与参数方程在直角坐标系中.直线经过点.其倾斜角为.在以原点为极点. 轴非负半轴为极轴的极坐标系中.曲线C的极坐标方程为． (Ⅰ)若直线与曲线C有公共点.求的取值范围, (Ⅱ)设为曲线C上任意一点.求的取值范围．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】选修44：坐标系与参数方程

在直角坐标系中，直线经过点，其倾斜角为，在以原点为极点，轴非负半轴为极轴的极坐标系中（取相同的长度单位），曲线C的极坐标方程为．
（Ⅰ）若直线与曲线C有公共点，求的取值范围；

（Ⅱ）设为曲线C上任意一点，求的取值范围．

【答案】（Ⅰ）（Ⅱ）

【解析】试题分析:（Ⅰ）先根据将曲线的极坐标方程化为直角坐标方程，再根据条件列出直线参数方程，代入曲线直角坐标方程，利用判别式列出不等式，解不等式可得的取值范围；（Ⅱ）曲线为一个圆，所以根据圆的参数方程可得，因此根据三角函数配角公式及正弦函数性质可求的取值范围.

试题解析：（Ⅰ）∵曲线的极坐标方程为，

∴曲线的直角坐标方程为

∵直线经过点，其倾斜角为，

∴直线的参数方程为（为参数）

将，代入整理得

∵直线与曲线有公共点，∴即或

∵ ∴的取值范围是

（Ⅱ）曲线的直角坐标方程为可化为

其参数方程为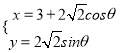（为参数）

∵为曲线上任意一点，∴

∴的取值范围是．

练习册系列答案

相关题目

【题目】沭阳县某水果店销售某种水果，经市场调查，该水果每日的销售量（单位：千克）与销售价格近似满足关系式，其中为常数，已知销售价格定为元千克时，每日可销售出该水果千克．

（1）求实数的值；

（2）若该水果的成本价格为元千克，要使得该水果店每日销售该水果获得最大利润，请你确定销售价格的值，并求出最大利润．

【题目】为参加学校的“我爱古诗词”知识竞赛，小王所在班级组织了一次古诗词知识测试，并将全班同学的分数（得分取正整数，满分为100分）进行统计，以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.

请根据以上频率分布表和频率分布直方图，回答下列问题：

（1）求出的值；

（2）老师说：“小王的测试成绩是全班同学成绩的中位数”，那么小王的测试成绩在什么范围内？

（3）若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛，请用：列表法或树状图求出小明、小敏同时被选中的概率.（注：五位同学请用表示，其中小明为，小敏为）

【题目】甲、乙两人各进行3次射击，甲每次击中目标的概率为，乙每次击中目标的概率为求：（1）甲恰好击中目标2次的概率；（2）乙至少击中目标2次的概率；

（3）乙恰好比甲多击中目标2次的概率

【题目】已知：函数且.

（1）求定义域；

（2）判断的奇偶性，并说明理由；

（3）求使的的解集．

【题目】在四棱锥P﹣ABCD中，AD∥BC，AD=AB=DC=BC=1，E是PC的中点，平面PAC⊥平面ABCD．

（1）证明：ED∥平面PAB；

（2）若PC=2，PA=，求二面角A﹣PC﹣D的余弦值．

【题目】为考察某种药物预防禽流感的效果，进行动物家禽试验，调查了100个样本，统计结果为：服用药的共有60个样本，服用药但患病的仍有20个样本，没有服用药且未患病的有20个样本.

（1）根据所给样本数据完成下面2×2列联表；

（2）请问能有多大把握认为药物有效？

	不得禽流感	得禽流感	总计
服药
不服药
总计

【题目】已知斜三棱柱的底面是直角三角形，，侧棱与底面所成角为，点在底面上身影落在上．

（1）求证：平面；

（2）若点恰为中点，且，求的大小；

（3）若，且当时，求二面角的大小．

【题目】性格色彩学创始人乐嘉是江苏电视台当红节目“非诚勿扰”的特约嘉宾，他的点评视角独特，语言犀利，给观众留下了深刻的印象，某报社为了了解观众对乐嘉的喜爱程度，随机调查了观看了该节目的140名观众，得到如下的列联表：（单位：名）

		男			女		总计
喜爱		40			60		100
不喜爱		20			20		40
总计		60			80		140
p（k2≥k0）	0.10		0.05	0.025		0.010		0.005
k0	2.705		3.841	5.024		6.635		7.879

（Ⅰ）从这60名男观众中按对乐嘉是否喜爱采取分层抽样，抽取一个容量为6的样本，问样本中喜爱与不喜爱的观众各有多少名？
（Ⅱ）根据以上列联表，问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱乐嘉有关?（精确到0.001）

（Ⅲ）从（Ⅰ）中的6名男性观众中随机选取两名作跟踪调查，求选到的两名观众都喜爱乐嘉的概率．

附：

试题分类