题目内容
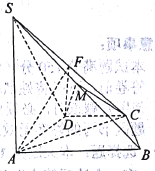
【题目】如图所示,四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 的中点,且
的中点,且![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当直线![]() 与底面
与底面![]() 成
成![]() 角时,求二面角
角时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)二面角![]() 的余弦值为
的余弦值为![]() .
.
【解析】试题分析:
(Ⅰ) 先证![]() ,得到
,得到![]() ,根据
,根据![]() 可得
可得![]() ,从而可得
,从而可得![]() ,于是平面
,于是平面![]() .(Ⅱ)建立空间直角坐标系,求出平面
.(Ⅱ)建立空间直角坐标系,求出平面![]() 平面
平面![]() 的法向量,然后求出两向量夹角的余弦值,从而可得二面角的余弦值.
的法向量,然后求出两向量夹角的余弦值,从而可得二面角的余弦值.
试题解析:
(Ⅰ)取![]() 的中点
的中点![]() ,连
,连![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
又![]() ,
, ![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,又
,又![]()
![]() ,又
,又![]()
![]() ,
,
又![]() ,
,
![]() 平面
平面![]() .
.
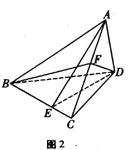
(Ⅱ)由(Ⅰ) 知![]() ,
, ![]() ,以
,以![]() 分别为
分别为![]() 轴建立空间直角坐标系,如图所示,设菱形
轴建立空间直角坐标系,如图所示,设菱形![]() 的边长为2,则
的边长为2,则![]() ,
, ![]() ,
,
因为直线![]() 与底面
与底面![]() 成
成![]() 角,即
角,即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
由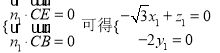 ,令
,令![]() ,则
,则![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
由 ,令
,令![]() ,则
,则![]() ,
,
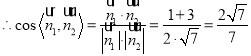 ,
,
由题可知二面角![]() 的平面角为钝角,
的平面角为钝角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径/ | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的概率);
表示相应事件的概率);
①![]() ;
;
②![]() ;
;
③![]()
评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备![]() 的性能等级.
的性能等级.
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
①从设备![]() 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() ;
;
②从样本中随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() .
.