题目内容
过原点的直线与圆x2+y2+4x+3=0相切,若切点在第三象限,则该直线的方程是( )
A. | B. | C. | D. |
C
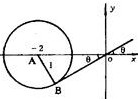
解析试题分析:圆方程可化为(x+2)2+y2=1,圆心为A(-2,0),半径为1,
结合图形得,得sinθ=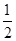 ,θ=
,θ=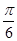 ,tanθ=
,tanθ=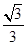 .即切线的斜率为
.即切线的斜率为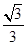 ,
,
所以,切线方程为 ,故选C。
,故选C。
考点:直线与圆的位置关系
点评:简单题,解题的关键是利用数形结合的思想,通过确定切线的斜率,达到解题目的。

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
过点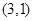 作圆
作圆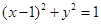 的两条切线,切点分别为
的两条切线,切点分别为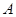 ,
,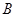 ,则直线
,则直线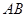 的方程为( )
的方程为( )
A. | B.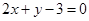 | C.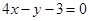 | D.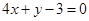 |
若直线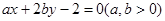 始终平分圆
始终平分圆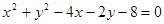 的周长,则
的周长,则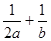 的最小值为( )
的最小值为( )
A.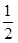 | B.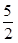 | C.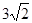 | D.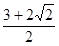 |
已知 ,则
,则 的取值范围是( )
的取值范围是( )
A.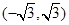 | B.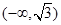 | C.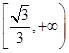 | D. |
过圆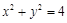 外一点
外一点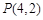 作圆的两条切线,切点分别为
作圆的两条切线,切点分别为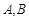 ,则
,则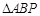 的外接圆方程是( )
的外接圆方程是( )
A.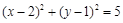 | B.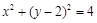 |
C.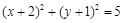 | D.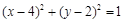 |
直线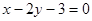 与圆
与圆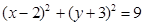 交于
交于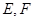 两点,则
两点,则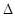
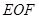 (
(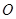 是原点)的面积为()
是原点)的面积为()
A.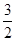 | B.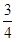 | C.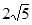 | D.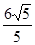 |
圆x2+y2+2x-4y=0的圆心坐标和半径分别是( )
| A.(1,-2),5 | B.(1,-2), |
| C.(-1,2),5 | D.(-1,2), |
若圆 上有且只有两个点到直线
上有且只有两个点到直线 的距离为1,则半径
的距离为1,则半径 的取值范围是( )
的取值范围是( )
A.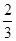 | B. | C. | D.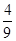 |
垂直于直线 且与圆
且与圆 相切于第一象限的直线方程是( )
相切于第一象限的直线方程是( )
A. | B. |
C. | D. |