题目内容
过圆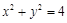 外一点
外一点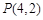 作圆的两条切线,切点分别为
作圆的两条切线,切点分别为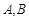 ,则
,则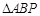 的外接圆方程是( )
的外接圆方程是( )
A.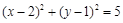 | B.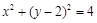 |
C.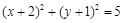 | D.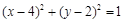 |
A
解析试题分析:根据题意,过圆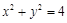 外一点
外一点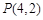 作圆的两条切线,切点分别为
作圆的两条切线,切点分别为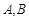 ,设直线PA:y-2=k(x-4),利用圆心到直线的距离为半径2,可知圆心与点P的中点为圆心(2,1),半径为OP距离的一半,即为
,设直线PA:y-2=k(x-4),利用圆心到直线的距离为半径2,可知圆心与点P的中点为圆心(2,1),半径为OP距离的一半,即为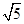 ,故可知答案为A.
,故可知答案为A.
考点:直线与圆
点评:主要是考查了直线与圆的位置关系的运用,属于基础题。

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
直线 截圆
截圆 得到的弦长为( )
得到的弦长为( )
| A.1 | B.2 | C. | D.2 |
经过点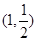 ,渐近线与圆
,渐近线与圆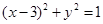 相切的双曲线的标准方程为( )
相切的双曲线的标准方程为( )
A.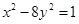 | B.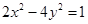 | C.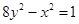 | D.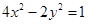 |
直线l:y=kx-3k与圆C:x +y
+y -4x=0的位置关系是
-4x=0的位置关系是
| A.l与C相交 | B.l与C相切 |
| C.l与C相离 | D.以上三个选项均有可能 |
过原点的直线与圆x2+y2+4x+3=0相切,若切点在第三象限,则该直线的方程是( )
A. | B. | C. | D. |
若圆C与圆(x+2)2+(y-1)2=1关于原点对称,则圆C的方程是( ).
| A.(x-2)2+(y+1)2=1 | B.(x-2)2+(y-1)2=1 |
| C.(x-1)2+(y+2)2=1 | D.(x+1) 2+(y-2)2=1 |
直线 与圆
与圆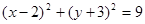 交于
交于 两点,则
两点,则
 (
( 是原点)的面积为
是原点)的面积为
A. | B. | C. | D. |
已知过点P(2,2) 的直线与圆 相切, 且与直线
相切, 且与直线 垂直, 则
垂直, 则 ( )
( )
A. | B.1 | C.2 | D. |
 的半径等于
的半径等于 ,圆心是抛物线
,圆心是抛物线 的焦点,经过点
的焦点,经过点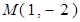
 将⊙
将⊙