题目内容
若实数a,b,c成等比数列,则函数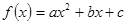 的图像与
的图像与 轴交点的个数为( )
轴交点的个数为( )
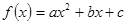 的图像与
的图像与 轴交点的个数为( )
轴交点的个数为( )| A.0个 | B.1个 | C.2个 | D.不能确定 |
A
由a,b,c成等比数列,得到b2=ac,且ac>0,
则b2-4ac=ac-4ac=-3ac<0,
所以函数f(x)=ax2+bx+c的图象与x轴的交点个数是0.
故答案为A
则b2-4ac=ac-4ac=-3ac<0,
所以函数f(x)=ax2+bx+c的图象与x轴的交点个数是0.
故答案为A

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
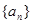 是非零等差数列,又
是非零等差数列,又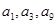 组成一个等比数列的前三项,则
组成一个等比数列的前三项,则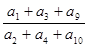 的值是 .
的值是 .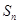 为等差数列
为等差数列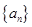 的前
的前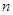 项和,若
项和,若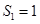 ,
,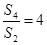 ,则
,则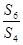 的值为( )
的值为( )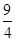
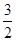
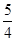
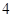
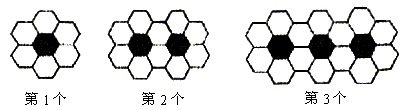
 中
中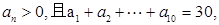 则
则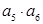 的最大值等于
的最大值等于 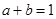 ,
,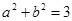 ,
,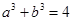 ,
,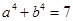 ,
, ,
,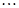 则
则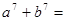 ( )
( )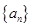 共有
共有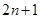 项,所有奇数项之和为
项,所有奇数项之和为 ,所有偶数项之和为
,所有偶数项之和为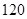 ,则n等于____________.
,则n等于____________.