题目内容
函数f(x)= x2-ln x的单调递减区间为________.
x2-ln x的单调递减区间为________.
 x2-ln x的单调递减区间为________.
x2-ln x的单调递减区间为________.(0,1]
由题意知,函数的定义域为(0,+∞),又由f′(x)=x-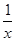 ≤0,解得0<x≤1,所以函数的单调递减区间为(0,1].
≤0,解得0<x≤1,所以函数的单调递减区间为(0,1].
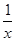 ≤0,解得0<x≤1,所以函数的单调递减区间为(0,1].
≤0,解得0<x≤1,所以函数的单调递减区间为(0,1].
练习册系列答案
相关题目
题目内容
 x2-ln x的单调递减区间为________.
x2-ln x的单调递减区间为________.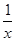 ≤0,解得0<x≤1,所以函数的单调递减区间为(0,1].
≤0,解得0<x≤1,所以函数的单调递减区间为(0,1].