题目内容
若函数f(x)=-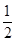
 +blnx在(1,+∞)上是减函数,求实数b的取值范围.
+blnx在(1,+∞)上是减函数,求实数b的取值范围.
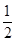
 +blnx在(1,+∞)上是减函数,求实数b的取值范围.
+blnx在(1,+∞)上是减函数,求实数b的取值范围.b≤1
由f(x)=-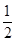
 +blnx,得f′(x)=-(x-2)+
+blnx,得f′(x)=-(x-2)+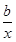 ,
,
由题意,知f′(x)≤0即-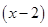 +
+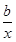 ≤0在(1,+∞)上恒成立,∴b≤
≤0在(1,+∞)上恒成立,∴b≤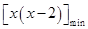 ,
,
当x∈(1,+∞)时, ∈(1,+∞),∴b≤1.
∈(1,+∞),∴b≤1.
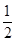
 +blnx,得f′(x)=-(x-2)+
+blnx,得f′(x)=-(x-2)+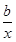 ,
,由题意,知f′(x)≤0即-
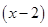 +
+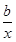 ≤0在(1,+∞)上恒成立,∴b≤
≤0在(1,+∞)上恒成立,∴b≤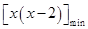 ,
,当x∈(1,+∞)时,
 ∈(1,+∞),∴b≤1.
∈(1,+∞),∴b≤1.
练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
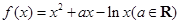 .
.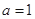 ,求函数
,求函数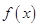 的单调区间;
的单调区间;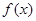 在区间
在区间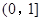 上是减函数,求实数
上是减函数,求实数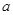 的取值范围;
的取值范围;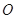 作曲线
作曲线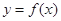 的切线,证明:切点的横坐标为
的切线,证明:切点的横坐标为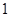 .
.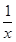 在
在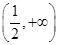 上是增函数,则a的取值范围是________.
上是增函数,则a的取值范围是________.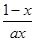 +ln x.
+ln x.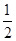 时,求f(x)在[1,e]上的最大值和最小值;
时,求f(x)在[1,e]上的最大值和最小值;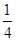 x在[1,e]上为增函数,求正实数a的取值范围.
x在[1,e]上为增函数,求正实数a的取值范围.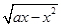 (a>0)的单调增区间为________,单调减区间为_______.
(a>0)的单调增区间为________,单调减区间为_______. x2-ln x的单调递减区间为________.
x2-ln x的单调递减区间为________.