题目内容
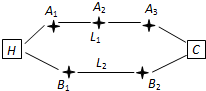 (2011•丰台区二模)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为
(2011•丰台区二模)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
(Ⅰ)若走L1路线,求最多遇到1次红灯的概率;
(Ⅱ)若走L2路线,求遇到红灯次数X的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.
关于概率统计问题,几次考查都没有将概率与统计图表结合起来,请老师们注意,在复练时要有意识的进行练习.
分析:(Ⅰ)设走L1路线最多遇到1次红灯为A事件,再根据题意求出其发生的概率为P(A)=
×(
)3+
×
×(
)2=
,即可得到答案.
(Ⅱ)依题意,X的可能取值为0,1,2.结合题意分别求出其发生的概率,即可得到随机变量X的分布列,进而求出X的期望.
(Ⅲ)根据题意可得:选择L1路线遇到红灯次数为Y,并且随机变量Y服从二项分布Y~B(3,
),即可根据有关公式求出Y的数学期望,进而能够做出正确的选择.
| C | 0 3 |
| 1 |
| 2 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)依题意,X的可能取值为0,1,2.结合题意分别求出其发生的概率,即可得到随机变量X的分布列,进而求出X的期望.
(Ⅲ)根据题意可得:选择L1路线遇到红灯次数为Y,并且随机变量Y服从二项分布Y~B(3,
| 1 |
| 2 |
解答:解:(Ⅰ)设走L1路线最多遇到1次红灯为A事件,
则P(A)=
×(
)3+
×
×(
)2=
. …(4分)
所以走L1路线,最多遇到1次红灯的概率为
.
(Ⅱ)依题意,X的可能取值为0,1,2. …(5分)
所以P(X=0)=(1-
)×(1-
)=
,P(X=1)=
×(1-
)+(1-
)×
=
,P(X=2)=
×
=
. …(8分)
所以随机变量X的分布列为:
所以EX=
×0+
×1+
×2=
. …(10分)
(Ⅲ)设选择L1路线遇到红灯次数为Y,随机变量Y服从二项分布,Y~B(3,
),
所以EY=3×
=
. …(12分)
因为EX<EY,所以选择L2路线上班最好. …(14分)
则P(A)=
| C | 0 3 |
| 1 |
| 2 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以走L1路线,最多遇到1次红灯的概率为
| 1 |
| 2 |
(Ⅱ)依题意,X的可能取值为0,1,2. …(5分)
所以P(X=0)=(1-
| 3 |
| 4 |
| 3 |
| 5 |
| 1 |
| 10 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 5 |
| 9 |
| 20 |
| 3 |
| 4 |
| 3 |
| 5 |
| 9 |
| 20 |
所以随机变量X的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 1 |
| 10 |
| 9 |
| 20 |
| 9 |
| 20 |
| 27 |
| 20 |
(Ⅲ)设选择L1路线遇到红灯次数为Y,随机变量Y服从二项分布,Y~B(3,
| 1 |
| 2 |
所以EY=3×
| 1 |
| 2 |
| 3 |
| 2 |
因为EX<EY,所以选择L2路线上班最好. …(14分)
点评:本题考查互斥事件的概率与相互独立事件的概率,以及考查离散型随机变量的分布列与数学期望,是一个和实际生活结合比较紧密的问题,此题属于中档题型,是高考命题的趋向.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目

 (2011•丰台区二模)如图所示,已知
(2011•丰台区二模)如图所示,已知