题目内容
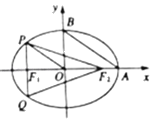
【题目】如图,过椭圆E:![]() (a>b>0)的左焦点F1作x轴的垂线交椭圆E于P,Q两点,点A,B是椭圆E的顶点,且AB∥OP,F2为右焦点,△PF2Q的周长为8.
(a>b>0)的左焦点F1作x轴的垂线交椭圆E于P,Q两点,点A,B是椭圆E的顶点,且AB∥OP,F2为右焦点,△PF2Q的周长为8.
(1)求椭圆E的方程;
(2)过点F1作直线l与椭圆E交于C,D两点,若△OCD的面积为![]() ,求直线l的方程.
,求直线l的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由题意,三角形的周长求出![]() 的值,再由AB∥OP,直线的斜率相等及a,c,b之间的关系求出椭圆的方程;
的值,再由AB∥OP,直线的斜率相等及a,c,b之间的关系求出椭圆的方程;
(2)设直线l的方程与椭圆联立,求出两根之和及两根之积,进而求出两根之差的绝对值,求出面积,再由椭圆求出直线方程.
(1)由题意得:4a=8,a=2,且 ,a2=b2+c2,b2=2,
,a2=b2+c2,b2=2,
所以椭圆的方程:![]() ;
;
(2)显然直线l的斜率不为零,
设l的方程为:x=my![]() ,C(x,y),D(x',y'),
,C(x,y),D(x',y'),
联立与椭圆的方程得:(2+m2)y2﹣2![]() my﹣1=0,y+y'
my﹣1=0,y+y'![]() ,yy'
,yy'![]() ,
,
S△OCD![]() |OF1||yC﹣yD|
|OF1||yC﹣yD|![]()
![]() 2
2![]() ,
,
∴由题意得:![]() ,整理得:5m4﹣34m2﹣7=0,
,整理得:5m4﹣34m2﹣7=0,
解得m2=7,所以m![]() ,
,
所以直线l的方程为:x![]() y
y![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目