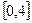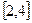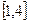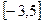题目内容
(本小题满分13分)
已知函数f(x)=-x2+ax-lnx(a∈R).
(1)求函数f(x)既有极大值又有极小值的充要条件;
(2)当函数f(x)在[,2]上单调时,求a的取值范围.
已知函数f(x)=-x2+ax-lnx(a∈R).
(1)求函数f(x)既有极大值又有极小值的充要条件;
(2)当函数f(x)在[,2]上单调时,求a的取值范围.
(1)a>2
(2)a≤2或a≥
解:(1)∵f′(x)=-2x+a-=(x>0),
∴f(x)既有极大值又有极小值?方程2x2-ax+1=0有两个不等的正实数根x1,x2.(3分)
∴a>2,
∴函数f(x)既有极大值又有极小值的充要条件是a>2.(6分)
(2)f′(x)=-2x+a-,令g(x)=2x+,
则g′(x)=2-,g(x)在[,)上递减,在(,2]上递增.(8分)
又g()=3,g(2)=,g()=2,
∴g(x)max=,g(x)min=2.(10分)
若f(x)在[,2]单调递增,则f′(x)≥0即a≥g(x),∴a≥.
若f(x)在[,2]单调递减,则f′(x)≤0,即a≤g(x),∴a≤2.
所以f(x)在[,2]上单调时,则a≤2或a≥.(13分)
∴f(x)既有极大值又有极小值?方程2x2-ax+1=0有两个不等的正实数根x1,x2.(3分)
∴a>2,
∴函数f(x)既有极大值又有极小值的充要条件是a>2.(6分)
(2)f′(x)=-2x+a-,令g(x)=2x+,
则g′(x)=2-,g(x)在[,)上递减,在(,2]上递增.(8分)
又g()=3,g(2)=,g()=2,
∴g(x)max=,g(x)min=2.(10分)
若f(x)在[,2]单调递增,则f′(x)≥0即a≥g(x),∴a≥.
若f(x)在[,2]单调递减,则f′(x)≤0,即a≤g(x),∴a≤2.
所以f(x)在[,2]上单调时,则a≤2或a≥.(13分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
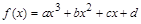 图象如图,则函数
图象如图,则函数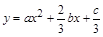 的单调递增区间为
的单调递增区间为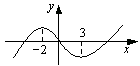
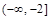
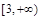
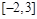

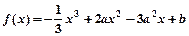
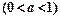
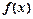 的单调区间、极值;
的单调区间、极值;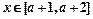 时,恒有
时,恒有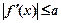 ,试确定
,试确定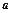 的取值范围。
的取值范围。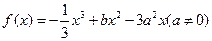 在
在 处取得极值
处取得极值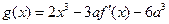 ,如果
,如果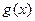 在区间(
在区间( 0,1)上存在极小值,求实数a的取值范围
0,1)上存在极小值,求实数a的取值范围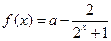 是奇函数
是奇函数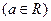 .
.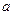 的值;
的值;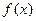 在(
在(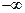 ,
,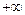 )上的单调性,并
)上的单调性,并 证明你的结论;
证明你的结论;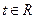 ,不
,不 等式
等式 恒成立,求实数
恒成立,求实数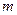 的取值范围.
的取值范围.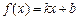 的图象与x、y轴分别相交于点A、 B,
的图象与x、y轴分别相交于点A、 B,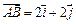 (
(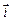 、
、 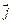 分别是与x、y轴正半轴同方向的单位向量), 函数
分别是与x、y轴正半轴同方向的单位向量), 函数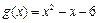
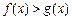 时,求函数
时,求函数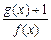 的最小值
的最小值 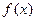 的图像经过点
的图像经过点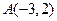 、
、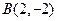 ,若函数
,若函数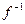 (
(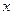 ),则不等式
),则不等式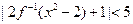 的解集为 。
的解集为 。 在区间
在区间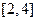 上是增函数,则实数
上是增函数,则实数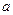 的取值范围是( )
的取值范围是( )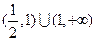
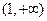
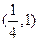
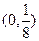

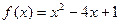 在定义域A上的值域为
在定义域A上的值域为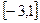 ,则区间A不可能为( )。
,则区间A不可能为( )。