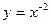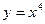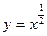题目内容
(本小题满分16分)已知函数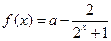 是奇函数
是奇函数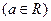 .
.
(Ⅰ)求实数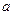 的值;
的值;
(Ⅱ)试判断函数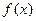 在(
在(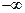 ,
,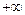 )上的单调性,并
)上的单调性,并 证明你的结论;
证明你的结论;
(Ⅲ)若对任意的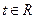 ,不
,不 等式
等式 恒成立,求实数
恒成立,求实数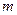 的取值范围.
的取值范围.
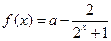 是奇函数
是奇函数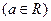 .
.(Ⅰ)求实数
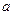 的值;
的值;(Ⅱ)试判断函数
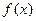 在(
在(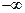 ,
,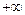 )上的单调性,并
)上的单调性,并 证明你的结论;
证明你的结论;(Ⅲ)若对任意的
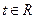 ,不
,不 等式
等式 恒成立,求实数
恒成立,求实数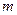 的取值范围.
的取值范围.(Ⅰ)1
(Ⅱ)
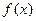 是
是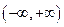 上的增函数
上的增函数(Ⅲ)
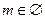
解:(Ⅰ)由题意可得: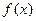 =
=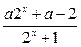
∵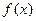 是奇函数 ∴
是奇函数 ∴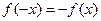
即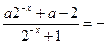

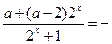
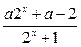
∴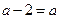 ,即
,即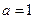 ……………………………………4分
……………………………………4分
即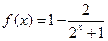
(Ⅱ)设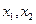 为
为 区间
区间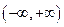 内的任意两个值,且
内的任意两个值,且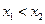 ,
,
则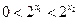 ,
,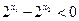 ,
,
∵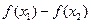 =
=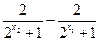 =
=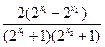
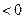
即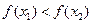 ∴
∴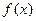 是
是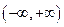 上的增函数.……………………
上的增函数.…………………… …10分
…10分
(Ⅲ)由(Ⅰ)、(Ⅱ) 知,
知,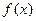 是
是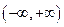 上的增函数,且是奇函数.
上的增函数,且是奇函数.
∵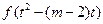
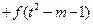
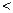 0
0
∴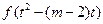
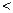
 =
=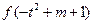
∴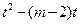
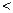
 …………………………13分
…………………………13分
即 对任意
对任意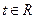 恒成立.
恒成立.
只需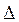 =
=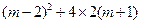 =
=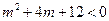 ,
,
解之得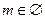 ……………………………………………………16分
……………………………………………………16分
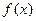 =
=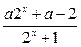
∵
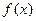 是奇函数 ∴
是奇函数 ∴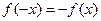
即
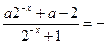

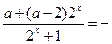
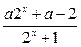
∴
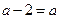 ,即
,即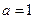 ……………………………………4分
……………………………………4分即
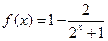
(Ⅱ)设
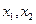 为
为 区间
区间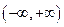 内的任意两个值,且
内的任意两个值,且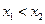 ,
,则
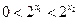 ,
,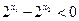 ,
,∵
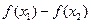 =
=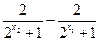 =
=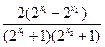
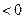
即
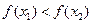 ∴
∴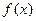 是
是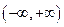 上的增函数.……………………
上的增函数.…………………… …10分
…10分(Ⅲ)由(Ⅰ)、(Ⅱ)
 知,
知,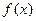 是
是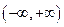 上的增函数,且是奇函数.
上的增函数,且是奇函数.∵
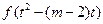
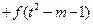
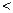 0
0∴
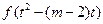
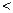
 =
=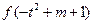
∴
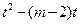
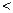
 …………………………13分
…………………………13分即
 对任意
对任意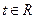 恒成立.
恒成立.只需
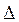 =
=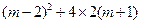 =
=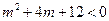 ,
,解之得
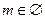 ……………………………………………………16分
……………………………………………………16分
练习册系列答案
相关题目
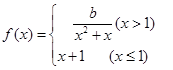 在R上连续,则
在R上连续,则 ( )
( )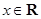 ,用
,用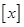 表示不超过
表示不超过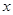 的最大整数,例如
的最大整数,例如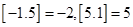 .则下列对函数
.则下列对函数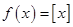 所具有的性质说法正确的有 ;(填上正确的编号)
所具有的性质说法正确的有 ;(填上正确的编号)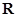 ,值域是
,值域是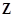 ;②若
;②若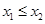 ,则
,则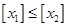 ;③
;③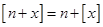 ,其中
,其中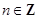 ;
;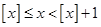 ;⑤
;⑤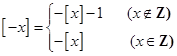
 是定义在
是定义在 上的增函数,对于任意的
上的增函数,对于任意的 ,都有
,都有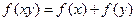 ,且满足
,且满足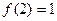 .
.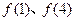 的值;
的值; 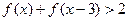 的
的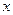 的取值范围.
的取值范围. +ax
+ax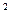 +bx+c的图像,如图所示,且与y=0在原点相切,若函数的极小值为–4,
+bx+c的图像,如图所示,且与y=0在原点相切,若函数的极小值为–4,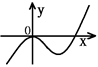
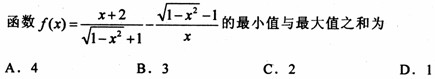
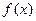 的单调增区间,且
的单调增区间,且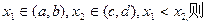
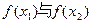 的大小关系为 ( )
的大小关系为 ( )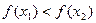
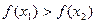
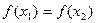
 上为单调递减的偶函数是( )
上为单调递减的偶函数是( )