题目内容
已知函数f(x)=()x,
函数y=f-1(x)是函数y=f(x)的反函数.
(1)若函数y=f-1(mx2+mx+1)的定义域为R,求实数m的取值范围;
(2)当x∈[-1,1]时,求函数y=[f(x)]2-2af(x)+3的最小值g(a);
(3)是否存在实数m>n>3,使得g(x)的定义域为[n,m],值域为[n2,m2]?若存在,求出m、n的值;若不存在,请说明理由
函数y=f-1(x)是函数y=f(x)的反函数.
(1)若函数y=f-1(mx2+mx+1)的定义域为R,求实数m的取值范围;
(2)当x∈[-1,1]时,求函数y=[f(x)]2-2af(x)+3的最小值g(a);
(3)是否存在实数m>n>3,使得g(x)的定义域为[n,m],值域为[n2,m2]?若存在,求出m、n的值;若不存在,请说明理由
(1)∵f-1(x)
=logx(x>0),
∴f-1(mx2+mx+1)
=log(mx2+mx+1),由题知,mx2+mx+1>0恒成立,
∴①当m=0时,1>0满足题意;
②当m≠0时,
应有
⇒0<m<4,
∴实数m的取值范围为
0≤m<4.
(2)∵x∈[-1,1],
∴()x∈[,3],
y=[f(x)]2-2af(x)+3
=[()x]2-2a()x+3
=[()x-a]2+3-a2,
当a<时,
ymin=g(a)=-;
当≤a≤3时,
ymin=g(a)=3-a2;
当a>3时,ymin=g(a)
=12-6a.
∴g(a)
=
(3)∵m>n>3,且g(x)=12-6x在(3,+∞)上是减函数.
又g(x)的定义域为[n,m],值域为[n2,m2].
∴
②-①得:6(m-n)=(m+n)(m-n)
∵m>n>3,∴m+n=6.但这与“m>n>3”矛盾.
∴满足题意的m、n不存在.
=logx(x>0),
∴f-1(mx2+mx+1)
=log(mx2+mx+1),由题知,mx2+mx+1>0恒成立,
∴①当m=0时,1>0满足题意;
②当m≠0时,
应有
⇒0<m<4,
∴实数m的取值范围为
0≤m<4.
(2)∵x∈[-1,1],
∴()x∈[,3],
y=[f(x)]2-2af(x)+3
=[()x]2-2a()x+3
=[()x-a]2+3-a2,
当a<时,
ymin=g(a)=-;
当≤a≤3时,
ymin=g(a)=3-a2;
当a>3时,ymin=g(a)
=12-6a.
∴g(a)
=
(3)∵m>n>3,且g(x)=12-6x在(3,+∞)上是减函数.
又g(x)的定义域为[n,m],值域为[n2,m2].
∴
②-①得:6(m-n)=(m+n)(m-n)
∵m>n>3,∴m+n=6.但这与“m>n>3”矛盾.
∴满足题意的m、n不存在.
略

练习册系列答案
相关题目
 与
与 的图象( )
的图象( ) 轴对称
轴对称 轴对称.
轴对称. 对称
对称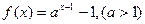 的反函数为
的反函数为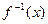 .
.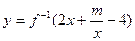 在区间
在区间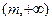 上单增,求实数
上单增,求实数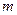 的取值范围;
的取值范围;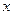 的方程
的方程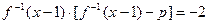 在
在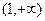 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数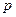 的取值范围.
的取值范围.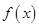 满足
满足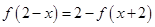 ,,若
,,若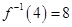 ,则
,则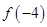 的值是
的值是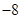
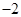
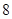
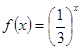
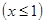 的反函数
的反函数 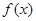 的图像与
的图像与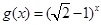 图像关于直线
图像关于直线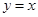 对称,则函数
对称,则函数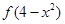 的单调增区间是__________
的单调增区间是__________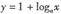 (a>0且
(a>0且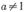 )的反函数是
)的反函数是

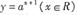

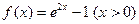 (
(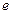 是自然对数的底数)的反函数为
是自然对数的底数)的反函数为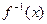 ,则有( )
,则有( )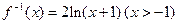
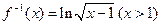
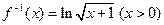
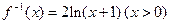
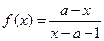 的反函数
的反函数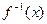 的对称中心为(-1,3),则实数a的值为 。
的对称中心为(-1,3),则实数a的值为 。