题目内容
设F（1，0），点M在x轴上，点P在y轴上，且
=2
，
•
=0；
（1）当点P在y轴上运动时，求点N的轨迹C的方程；
（2）设A（x1，y1），B（x2，y2），D（x3，y3）是曲线C上除去原点外的不同三点，且
，
，
成等差数列，当线段AD的垂直平分线与x轴交于点E（3，0）时，求点B的坐标．
| MN |
| MP |
| PM |
| PF |
（1）当点P在y轴上运动时，求点N的轨迹C的方程；
（2）设A（x1，y1），B（x2，y2），D（x3，y3）是曲线C上除去原点外的不同三点，且
| |AF| |
| |BF| |
| |DF| |
分析：（1）设出N的坐标，确定
，
的坐标，利用
•
=0，可得点N的轨迹C的方程；
（2）先确定线段AD的垂直平分线的斜率、AD的斜率，可得方程，利用点B在抛物线上，即可求得点B的坐标．
| PM |
| PF |
| PM |
| PF |
（2）先确定线段AD的垂直平分线的斜率、AD的斜率，可得方程，利用点B在抛物线上，即可求得点B的坐标．
解答：解：（1）设N（x，y），由
=2
，得点P为线段MN的中点，∴P（0，
），M（-x，0），
∴
=（-x，-
），
=（1，-
）．
由
•
=-x+
=0，得y2=4x．
即点N的轨迹方程为y2=4x．
（2）由抛物线的定义，知|AF|=x1+1，|BF|=x2+1，|DF|=x3+1，
∵
，
，
成等差数列，
∴2x2+2=x1+1+x3+1，即x2=
．
∵线段AD的中点为（
，
），且线段AD的垂直平分线与x轴交于点E（3，0），
∴线段AD的垂直平分线的斜率为k=
．
又kAD=
，∴•
•
=-1，
即
=-1．
∵x1≠x3，∴x1+x3=2，又x2=
，∴x2=1．
∵点B在抛物线上，
∴B（1，2）或（1，-2）．
| MN |
| MP |
| y |
| 2 |
∴
| PM |
| y |
| 2 |
| PF |
| y |
| 2 |
由
| PM |
| PF |
| y2 |
| 4 |
即点N的轨迹方程为y2=4x．
（2）由抛物线的定义，知|AF|=x1+1，|BF|=x2+1，|DF|=x3+1，
∵
| |AF| |
| |BF| |
| |DF| |
∴2x2+2=x1+1+x3+1，即x2=
| x1+x3 |
| 2 |
∵线段AD的中点为（
| x1+x3 |
| 2 |
| y1+y3 |
| 2 |
∴线段AD的垂直平分线的斜率为k=
| ||
|
又kAD=
| y3-y1 |
| x3-x1 |
| y3-y1 |
| x3-x1 |
| y1+y3 |
| x1+x3-6 |
即
| 4x3-4x1 |
| (x32-x12)-6(x3-x1) |
∵x1≠x3，∴x1+x3=2，又x2=
| x1+x3 |
| 2 |
∵点B在抛物线上，
∴B（1，2）或（1，-2）．
点评：本题考查轨迹方程，考查等差数列，考查向量知识的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
=2
，
=0；
，
，
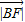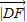成等差数列，当线段AD的垂直平分线与x轴交于点E（3，0）时，求点B的坐标．
．
成等差数列，当AD的垂直平分线与x轴交于点E（3，0）时，求点B的坐标．
是曲线C上的点，且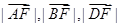
成等差数列，当AD的垂直平分线与x轴交于点E（3，0）时，求点B的坐标。