题目内容
设F(1,0),点M在x轴上,点P在y轴上,且
(1)当点P在y轴上运动时,求点N的轨迹C的方程;
(2)设 是曲线C上的点,且
是曲线C上的点,且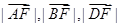 成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标。
成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标。
【解析】本试题主要是对于圆锥曲线的综合考查。首先求解轨迹方程,利用向量作为工具表示向量的坐标,进而达到关系式的求解。第二问中利用数列的知识和直线方程求解点的坐标。
【答案】
解:(1)设 ,则由
,则由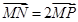 得P为MN的中点,
得P为MN的中点,
所以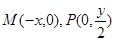 …………1分
…………1分
又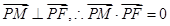
 ,…………3分
,…………3分
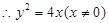 …………5分
…………5分
(2)由(1)知 为曲线C的焦点,由抛物线定义知抛物线上任一点
为曲线C的焦点,由抛物线定义知抛物线上任一点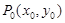 到F的距离等于其到准线的距离,即
到F的距离等于其到准线的距离,即 …………6分
…………6分
故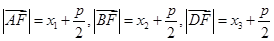 ,又
,又 成等差数列
成等差数列
得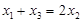 …………7分
…………7分
直线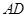 的斜率
的斜率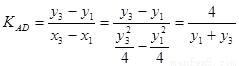
 …………9分
…………9分
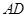 的中垂线方程为
的中垂线方程为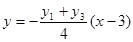 …………10分
…………10分
又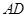 的中点
的中点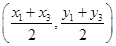 在直线上,代入上式,得
在直线上,代入上式,得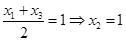 …11分
…11分
故所求点B的坐标为

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 =2
=2 ,
, =0;
=0; ,
,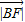 ,
,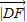 成等差数列,当线段AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标.
成等差数列,当线段AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标. .
. 成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标.
成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标.