题目内容
已知数列{an}满足递推式an=2an-1+1(n≥2),其中a4=15.
(Ⅰ)求a1,a2,a3;
(Ⅱ)求证数列{an+1}是等比数列,并求数列{an}的通项公式;
(Ⅲ)已知数列{bn}有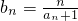 求数列{bn}的前n项和Sn.
求数列{bn}的前n项和Sn.
(Ⅰ)解:由an=2an-1+1(n≥2),及a4=15,知a4=2a3+1得a3=7
同理得a2=3,a1=1------(3分)
(Ⅱ)证明:由an=2an-1+1(n≥2)得an+1=2(an-1+1)
所以,数列{an+1}是首项为a1+1=2,公比为2的等比数列
所以,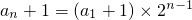 ,
,
所以,数列{an}的通项公式为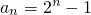 ------(3分)
------(3分)
(Ⅲ)解:∵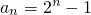 ,∴
,∴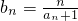 =
=
∴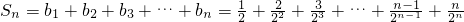 ①
①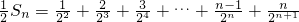 ②
②
由①-②错位相减得: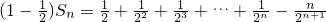
故: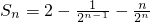 ------(4分)
------(4分)
分析:(Ⅰ)由an=2an-1+1(n≥2),a4=15,代入计算,可求a1,a2,a3;
(Ⅱ)由an=2an-1+1(n≥2)得an+1=2(an-1+1),即可得到数列{an+1}是等比数列,从而可求数列{an}的通项公式;
(Ⅲ)利用错位相减法,可求数列{bn}的前n项和Sn.
点评:本题考查数列递推式,考查等比数列的证明,考查错位相减法的运用,考查学生的计算能力,属于中档题.
同理得a2=3,a1=1------(3分)
(Ⅱ)证明:由an=2an-1+1(n≥2)得an+1=2(an-1+1)
所以,数列{an+1}是首项为a1+1=2,公比为2的等比数列
所以,
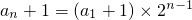 ,
,所以,数列{an}的通项公式为
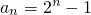 ------(3分)
------(3分)(Ⅲ)解:∵
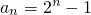 ,∴
,∴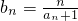 =
=
∴
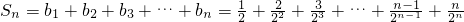 ①
①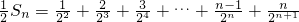 ②
②由①-②错位相减得:
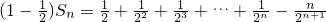
故:
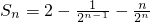 ------(4分)
------(4分)分析:(Ⅰ)由an=2an-1+1(n≥2),a4=15,代入计算,可求a1,a2,a3;
(Ⅱ)由an=2an-1+1(n≥2)得an+1=2(an-1+1),即可得到数列{an+1}是等比数列,从而可求数列{an}的通项公式;
(Ⅲ)利用错位相减法,可求数列{bn}的前n项和Sn.
点评:本题考查数列递推式,考查等比数列的证明,考查错位相减法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目