题目内容
已知函数
在x1处取得极大值,在x2处取得极小值,且x1∈（－1，1），x2∈（1，2），则2a+b的取值范围是（ ）
在x1处取得极大值,在x2处取得极小值,且x1∈（－1，1），x2∈（1，2），则2a+b的取值范围是（ ）| A．（－7，2） | B．（－7，3） | C．（2，3） | D．（－1，2） |
B
∵f′(x)= x2+bx－a,
∴据题意知, f′(x1)= f′(x2)=0,
又据二次函数知, f′(－1) ＞0 且f′(1)＜0且f′(2)＞0
即
如图为(a,b)之可行域,A(1,0),B(2,－1),(－2,－3)．把A,B,C三点坐标代入2a+b得2,3,－7
所以2a+b的范围为(－7,3)
∴据题意知, f′(x1)= f′(x2)=0,
又据二次函数知, f′(－1) ＞0 且f′(1)＜0且f′(2)＞0
即
如图为(a,b)之可行域,A(1,0),B(2,－1),(－2,－3)．把A,B,C三点坐标代入2a+b得2,3,－7
所以2a+b的范围为(－7,3)
练习册系列答案
相关题目
表示的平面区域为( )
、
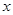满足约束条件
，则
的最小值是 .
那么2x-y的最大值为
满足方程C：
，则
的最大值是___________．
若z的最大值为12，则实数k= _________ ．
，满足
，x≥1，则
的最大值为 ．
、
满足条件
，则
的最大值为_______.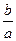
的取值范围是 ．