题目内容
设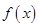 是定义在
是定义在 上以2为周期的偶函数,已知
上以2为周期的偶函数,已知 ,
,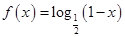 ,则函数
,则函数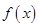 在
在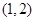 上( )
上( )
A.是增函数且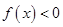 | B.是增函数且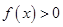 |
C.是减函数且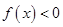 | D.是减函数且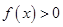 |
D
解析试题分析:设 x∈(-1,0),则-x∈(0,1),故 f(-x)= .
.
又f(x)是定义在R上以2为周期的偶函数,故 f(x)= .
.
再令 1<x<2,则-1<x-2<0,∴f(x-2)= ,∴f(x)=
,∴f(x)=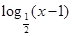 ,
,
由1<x<2 可得 0<x-1<1,
故函数f(x)在(1,2)上是减函数,且f(x)>0,
故选D.
考点:本题主要考查函数的单调性,奇偶性和周期性,对数函数的性质。
点评:典型题,利用奇偶性求函数的解析式,是常用处理方法,求出函数f(x)在(1,2)上 的解析式,是解题的关键。

练习册系列答案
相关题目
函数 的单调递减区间是( )
的单调递减区间是( )
A. | B. | C. | D. |
下列各组函数中表示同一函数的是 ( )
A.f(x)=x与g(x)=( )2 )2 | B.f(x)=|x|与g(x)= |
C.f(x)=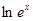 与g(x)= 与g(x)= | D.f(x)= 与g(t)=t+1(t≠1) 与g(t)=t+1(t≠1) |
设偶函数 的定义域为R,当
的定义域为R,当 时,
时, 是增函数,则
是增函数,则
的大小关系是( )
A. > >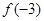 > >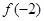 | B. > >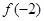 > >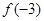 |
C. < <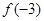 < <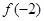 | D. < <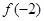 < <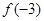 |
已知函数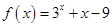 的零点为
的零点为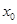 , 则
, 则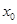 所在区间为( )
所在区间为( )
A. | B.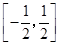 | C.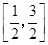 | D.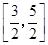 |
函数 的图象与直线
的图象与直线 的公共点数目是( )
的公共点数目是( )
A. | B. | C. 或 或 | D. 或 或 |
已知函数 ,给定区间E,对任意
,给定区间E,对任意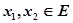 ,当
,当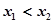 时,总有
时,总有 则下列区间可作为E的是( )
则下列区间可作为E的是( )
| A.(-3,-1) | B.(-1,0) | C.(1,2) | D.(3,6) |
已知函数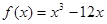 ,若
,若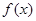 在区间
在区间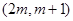 上单调递减,则实数
上单调递减,则实数 的取值范围是( )
的取值范围是( )
A.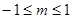 | B.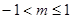 | C.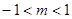 | D.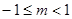 |
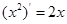 ,
, ,
,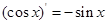 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在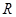 上的函数
上的函数 满足
满足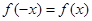 ,记
,记 为
为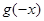 =( )
=( )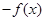 C
C