题目内容
已知函数 ,给定区间E,对任意
,给定区间E,对任意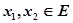 ,当
,当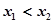 时,总有
时,总有 则下列区间可作为E的是( )
则下列区间可作为E的是( )
| A.(-3,-1) | B.(-1,0) | C.(1,2) | D.(3,6) |
A
解析试题分析:根据题意由于函数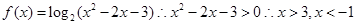 ,同时,任意
,同时,任意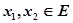 ,当
,当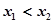 时,总有
时,总有 则说明函数在定义域内是递减的,因此求解的是函数的减区间,外层是递增的,则求解内层的减区间即可,对称轴x=1,那么开口向上,故可知答案为A.
则说明函数在定义域内是递减的,因此求解的是函数的减区间,外层是递增的,则求解内层的减区间即可,对称轴x=1,那么开口向上,故可知答案为A.
考点:函数的单调性
点评:解决的关键是根据给定的单调性的定义来判定函数的单调性,进而得到对应的复合函数 单调区间,属于基础题。

练习册系列答案
相关题目
当 时,函数
时,函数 取得最小值,则函数
取得最小值,则函数 是( )
是( )
A.奇函数且图像关于点 对称 对称 |
B.偶函数且图像关于点 对称 对称 |
C.奇函数且图像关于直线 对称 对称 |
D.偶函数且图像关于点 对称 对称 |
设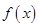 是定义在
是定义在 上以2为周期的偶函数,已知
上以2为周期的偶函数,已知 ,
,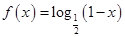 ,则函数
,则函数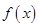 在
在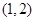 上( )
上( )
A.是增函数且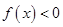 | B.是增函数且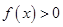 |
C.是减函数且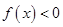 | D.是减函数且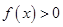 |
如图,矩形纸板ABCD的顶点A、B分别在正方形边框EOFG的边OE、OF上,当点B在OF边上进行左右运动时,点A随之在OE上进行上下运动.若AB=8,BC=3,运动过程中,则点D到点O距离的最大值为
A. | B.9 | C. | D. |
若函数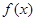 的定义域是[0,4],则函数
的定义域是[0,4],则函数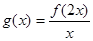 的定义域是( )
的定义域是( )
| A.[ 0, 2] | B.(0,2) | C.(0,2] | D.[0,) |
已知函数 ,则
,则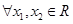 且
且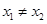 ,有
,有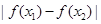 与
与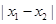 的大小关系为
的大小关系为
A.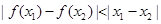 | B.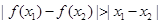 |
C.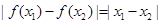 | D.不能确定 |
设函数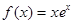 ,则( )
,则( )
A.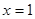 为 为 的极大值点 的极大值点 | B.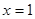 为 为 的极小值点 的极小值点 |
C. 为 为 的极大值点 的极大值点 | D. 为 为 的极小值点 的极小值点 |
已知函数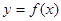 在R上是增函数,且
在R上是增函数,且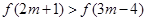 ,则
,则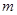 的取值范围是( )
的取值范围是( )
A.(-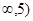 | B.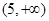 | C.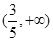 | D.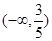 |