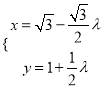题目内容
【题目】若Sn=cos 
+cos 
+…+cos 
（n∈N+），则在S1 ， S2 ， …，S2015中，正数的个数是（ ）
A.882
B.756
C.750
D.378
【答案】B
【解析】解：∵cos 
＞0，cos 
＞0，cos 
＞0， 
=0， 
=﹣cos ＜0， 
=﹣cos ＜0， 
=﹣cos ＜0，cos 
=﹣1＜0， 
=﹣cos ＜0， 
=﹣cos ＜0， 
=﹣cos ＜0， 
=0，cos 
=cos ＞0，cos 
=cos ＞0，cos 
=cos ＞0，cos2π=1．
∴S1＞0，…，S6＞0，S7=0，S8＜0，…，S15＜0，S16=0．
在S1 ， S2 ， …，S16中，正数的个数是6个．
由三角函数的周期性，可得：在S1 ， S2 ， …，S2000 ， 正数的个数有750项．
S2001 ， …，S2015中，正数的个数也6项．
在S1 ， S2 ， …，S2015中，正数的个数是756．
故选：B．
【考点精析】根据题目的已知条件，利用数列的前n项和的相关知识可以得到问题的答案，需要掌握数列{an}的前n项和sn与通项an的关系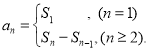
．
【题目】“累积净化量
”是空气净化器质量的一个重要衡量指标，它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量，以克表示，根据
《空气净化器》国家标准，对空气净化器的累计净化量有如下等级划分：
累积净化量（克） |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器（共5000台）的质量，随机抽取
台机器作为样本进行估计，已知这台机器的累积净化量都分布在区间
中，按照
、
、
、
、
均匀分组，其中累积净化量在的所有数据有：4.5,4.6,5.2,5.3,5.7和5.9，并绘制了频率分布直方图，如图所示：
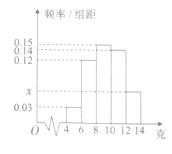
（1）求的值及频率分布直方图中
的值；
（2）以样本估计总体，试估计这批空气净化器（共5000台）中等级为
的空气净化器有多少台？
（3）从累积净化量在的样本中随机抽取2台，求恰好有1台等级为的概率.
