Question

【题目】已知函数为正常数．

⑴若，且，求函数的单调增区间；

⑵在⑴中当时，函数的图象上任意不同的两点，线段的中点为，记直线的斜率为，试证明： ．

⑶若，且对任意的， ，都有，求的取值范围．

Answer 1

【答案】（1）单调增区间为. （2）见解析（3）

【解析】试题分析：（1）由题意先求出 的解析式，然后求其导函数，令导函数大于 ，解出的即为函数的增区间；（2）对于当 时，先求出 的解析式，然后求导函数，得到 ，在利用斜率公式求出过这两点的斜率公式，利用构造函数并利用构造函数的单调性比较大小；（3）因为 ，且对任意 ，都有 ，先写出 的解析式，利用该函数的单调性把问题转化为恒成立问题进行求解.

试题解析：⑴∵a，令得x>3或0<x<,∴函数的单调增区间为.

⑵证明：当时∴, ∴,又

不妨设 ， 要比较与的大小，即比较与的大小，又∵，∴ 即比较与的大小． 令,则,

∴在上位增函数．又，∴， ∴，即

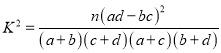⑶∵，∴ 由题意得在区间上是减函数．

当， ∴由在恒成立．设， ，则∴在上为增函数，∴.

当，∴ 由

在恒成立

设 ， 为增函数,∴综上：a的取值范围为