题目内容
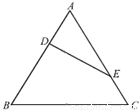
等边三角形ABC的边长为3,点D、E分别是边AB、AC上的点,且满足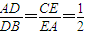 (如图1).将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B成直二面角,连结A1B、A1C (如图2).
(如图1).将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B成直二面角,连结A1B、A1C (如图2).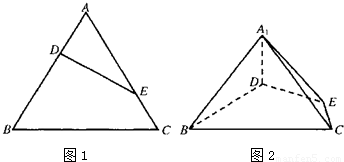
(1)求证:A1D丄平面BCED;
(2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60?若存在,求出PB的长;若不存在,请说明理由.
【答案】分析:(1)等边△ABC中,根据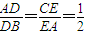 得到AD=1且AE=2,由余弦定理算出DE=
得到AD=1且AE=2,由余弦定理算出DE=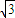 ,从而得到AD2+DE2=AE2,所以AD⊥DE.结合题意得平面A1DE⊥平面BCDE,利用面面垂直的性质定理,可证出A1D丄平面BCED;
,从而得到AD2+DE2=AE2,所以AD⊥DE.结合题意得平面A1DE⊥平面BCDE,利用面面垂直的性质定理,可证出A1D丄平面BCED;
(2)作PH⊥BD于点H,连接A1H、A1P,由A1D丄平面BCED得A1D丄PH,所以PH⊥平面A1BD,可得∠PA1H是直线PA1与平面A1BD所成的角,即∠PA1H=60°.设PB=x(0≤x≤3),分别在Rt△BA1H、Rt△PA1H和Rt△DA1H中利用三角函数定义和勾股定理,建立等量关系得12+(2- x)2=(
x)2=( x)2,解之得x=
x)2,解之得x= ,从而得到在BC上存在点P且当PB=
,从而得到在BC上存在点P且当PB= 时,直线PA1与平面A1BD所成的角为60°.
时,直线PA1与平面A1BD所成的角为60°.
解答:解:(1)∵正△ABC的边长为3,且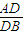 =
=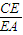 =
=
∴AD=1,AE=2,
△ADE中,∠DAE=60°,由余弦定理,得
DE=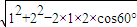 =
=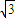
∵AD2+DE2=4=AE2,∴AD⊥DE.
折叠后,仍有A1D⊥DE
∵二面角A1-DE-B成直二面角,∴平面A1DE⊥平面BCDE
又∵平面A1DE∩平面BCDE=DE,A1D?平面A1DE,A1D⊥DE
∴A1D丄平面BCED;
(2)假设在线段BC上存在点P,使直线PA1与平面A1BD所成的角为60°
如图,作PH⊥BD于点H,连接A1H、A1P
由(1)得A1D丄平面BCED,而PH?平面BCED
所以A1D丄PH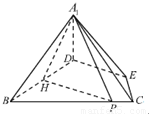
∵A1D、BD是平面A1BD内的相交直线,
∴PH⊥平面A1BD
由此可得∠PA1H是直线PA1与平面A1BD所成的角,即∠PA1H=60°
设PB=x(0≤x≤3),则BH=PBcos60°=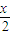 ,PH=PBsin60°=
,PH=PBsin60°=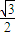 x
x
在Rt△PA1H中,∠PA1H=60°,所以A1H=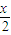 ,
,
在Rt△DA1H中,A1D=1,DH=2- x
x
由A1D2+DH2=A1H2,得12+(2- x)2=(
x)2=( x)2
x)2
解之得x= ,满足0≤x≤3符合题意
,满足0≤x≤3符合题意
所以在线段BC上存在点P,使直线PA1与平面A1BD所成的角为60°,此时PB= .
.
点评:本题给出平面翻折问题,求证直线与平面垂直并探索了直线与平面所成角的问题,着重考查了线面垂直、面面垂直的判定与性质和直线与平面所成角的求法等知识,属于中档题.
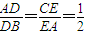 得到AD=1且AE=2,由余弦定理算出DE=
得到AD=1且AE=2,由余弦定理算出DE=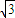 ,从而得到AD2+DE2=AE2,所以AD⊥DE.结合题意得平面A1DE⊥平面BCDE,利用面面垂直的性质定理,可证出A1D丄平面BCED;
,从而得到AD2+DE2=AE2,所以AD⊥DE.结合题意得平面A1DE⊥平面BCDE,利用面面垂直的性质定理,可证出A1D丄平面BCED;(2)作PH⊥BD于点H,连接A1H、A1P,由A1D丄平面BCED得A1D丄PH,所以PH⊥平面A1BD,可得∠PA1H是直线PA1与平面A1BD所成的角,即∠PA1H=60°.设PB=x(0≤x≤3),分别在Rt△BA1H、Rt△PA1H和Rt△DA1H中利用三角函数定义和勾股定理,建立等量关系得12+(2-
 x)2=(
x)2=( x)2,解之得x=
x)2,解之得x= ,从而得到在BC上存在点P且当PB=
,从而得到在BC上存在点P且当PB= 时,直线PA1与平面A1BD所成的角为60°.
时,直线PA1与平面A1BD所成的角为60°.解答:解:(1)∵正△ABC的边长为3,且
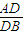 =
=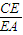 =
=

∴AD=1,AE=2,
△ADE中,∠DAE=60°,由余弦定理,得
DE=
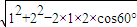 =
=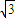
∵AD2+DE2=4=AE2,∴AD⊥DE.
折叠后,仍有A1D⊥DE
∵二面角A1-DE-B成直二面角,∴平面A1DE⊥平面BCDE
又∵平面A1DE∩平面BCDE=DE,A1D?平面A1DE,A1D⊥DE
∴A1D丄平面BCED;
(2)假设在线段BC上存在点P,使直线PA1与平面A1BD所成的角为60°
如图,作PH⊥BD于点H,连接A1H、A1P
由(1)得A1D丄平面BCED,而PH?平面BCED
所以A1D丄PH

∵A1D、BD是平面A1BD内的相交直线,
∴PH⊥平面A1BD
由此可得∠PA1H是直线PA1与平面A1BD所成的角,即∠PA1H=60°
设PB=x(0≤x≤3),则BH=PBcos60°=
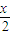 ,PH=PBsin60°=
,PH=PBsin60°=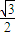 x
x在Rt△PA1H中,∠PA1H=60°,所以A1H=
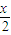 ,
,在Rt△DA1H中,A1D=1,DH=2-
 x
x由A1D2+DH2=A1H2,得12+(2-
 x)2=(
x)2=( x)2
x)2解之得x=
 ,满足0≤x≤3符合题意
,满足0≤x≤3符合题意所以在线段BC上存在点P,使直线PA1与平面A1BD所成的角为60°,此时PB=
 .
.点评:本题给出平面翻折问题,求证直线与平面垂直并探索了直线与平面所成角的问题,着重考查了线面垂直、面面垂直的判定与性质和直线与平面所成角的求法等知识,属于中档题.

练习册系列答案
相关题目
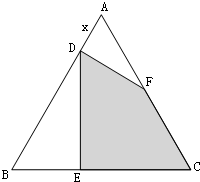 如图,等边三角形ABC的边长为6,在AB上截取AD,过D点作DF⊥AB,交AC于点F,过D点作DE⊥BC,交BC于点E.设AD=x,四边形DECF的面积为y.
如图,等边三角形ABC的边长为6,在AB上截取AD,过D点作DF⊥AB,交AC于点F,过D点作DE⊥BC,交BC于点E.设AD=x,四边形DECF的面积为y. 已知等边三角形ABC的边长为2,⊙A的半径为1,PQ为⊙A的任意一条直径,则
已知等边三角形ABC的边长为2,⊙A的半径为1,PQ为⊙A的任意一条直径,则