题目内容
等边三角形ABC的边长为4,M、N分别为AB、AC的中点,沿MN将△AMN折起,使得面AMN与面MNCB所处的二面角为30°,则四棱锥A-MNCB的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
分析:沿MN将△AMN折起,使得面AMN与面MNCB所处的二面角为30°,求出四棱锥A-MNCB的高,底面面积,即可求出四棱锥的体积.
解答: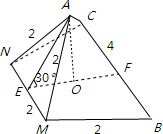 解:由题意画出图形如图,取MN,BC的中点E,F,易知∠AEF=30°,
解:由题意画出图形如图,取MN,BC的中点E,F,易知∠AEF=30°,
由题意可知AE=
,棱锥的高为AO=
底面面积为:
×
×42=3
则四棱锥A-MNCB的体积为:
×
×3
=
故选A
 解:由题意画出图形如图,取MN,BC的中点E,F,易知∠AEF=30°,
解:由题意画出图形如图,取MN,BC的中点E,F,易知∠AEF=30°,由题意可知AE=
| 3 |
| ||
| 2 |
底面面积为:
| 3 |
| 4 |
| ||
| 4 |
| 3 |
则四棱锥A-MNCB的体积为:
| 1 |
| 3 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
故选A
点评:本题是基础题,考查空间想象能力,平面图形的折叠问题,注意同一个半平面上的几何关系不变,考查计算能力,是常考题型.

练习册系列答案
相关题目
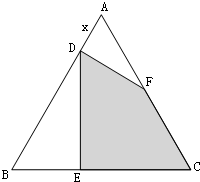 如图,等边三角形ABC的边长为6,在AB上截取AD,过D点作DF⊥AB,交AC于点F,过D点作DE⊥BC,交BC于点E.设AD=x,四边形DECF的面积为y.
如图,等边三角形ABC的边长为6,在AB上截取AD,过D点作DF⊥AB,交AC于点F,过D点作DE⊥BC,交BC于点E.设AD=x,四边形DECF的面积为y. 已知等边三角形ABC的边长为2,⊙A的半径为1,PQ为⊙A的任意一条直径,则
已知等边三角形ABC的边长为2,⊙A的半径为1,PQ为⊙A的任意一条直径,则