题目内容
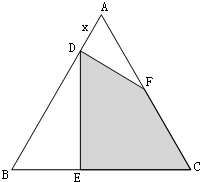
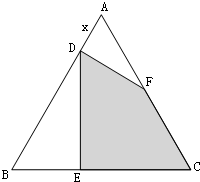 如图,等边三角形ABC的边长为6,在AB上截取AD,过D点作DF⊥AB,交AC于点F,过D点作DE⊥BC,交BC于点E.设AD=x,四边形DECF的面积为y.
如图,等边三角形ABC的边长为6,在AB上截取AD,过D点作DF⊥AB,交AC于点F,过D点作DE⊥BC,交BC于点E.设AD=x,四边形DECF的面积为y.(1)写出y关于x的函数解析式并指出函数的定义域;
(2)当AD等于多少时,y有最大值,并求出最大值.
分析:(1)利用三角形的面积公式求出三个三角形的面积,然后用大三角形的面积减去小三角形的面积.
(2)通过配方,求出二次函数的对称轴,然后求出二次函数的最值.
(2)通过配方,求出二次函数的对称轴,然后求出二次函数的最值.
解答:解:(1)y=S△ABC-S△ADF-S△BDE=-
x2+
x+
(4分)
函数的定义域为(0,3)(5分)
(2)y=-
(x-
)2+
(7分)
∴AD等于
时,y取得最大值
.(8分)
5
| ||
| 8 |
3
| ||
| 2 |
9
| ||
| 2 |
函数的定义域为(0,3)(5分)
(2)y=-
5
| ||
| 8 |
| 6 |
| 5 |
27
| ||
| 5 |
∴AD等于
| 6 |
| 5 |
27
| ||
| 5 |
点评:求二次函数的最值问题,关键是求出二次函数的对称轴,然后判断出二次函数的单调性,求出最值.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
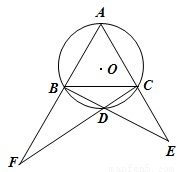
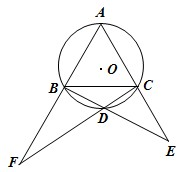 (2012•盐城二模)选修4-1:几何证明选讲:
(2012•盐城二模)选修4-1:几何证明选讲: 选修4-1:几何证明选讲:
选修4-1:几何证明选讲: