题目内容
已知等边三角形ABC的边长为2，⊙A的半径为1，PQ为⊙A的任意一条直径，则| BP |
| CQ |
| AP |
| CB |
1
1
．分析：先根据向量的三角形法则得到
•
-
•
=(
-
)•(
-
)-
•(
-
)，再结合
=-
以及等边三角形ABC的边长为2，⊙A的半径为1即可得到答案．
| BP |
| CQ |
| AP |
| CB |
| AP |
| AB |
| AQ |
| AC |
| AP |
| AB |
| AC |
| AQ |
| AP |
解答：解：由于
•
-
•
=(
-
)•(
-
)-
•(
-
)，
而
=-
，
则
•
-
•
=(
-
)•(-
-
)-
•(
-
)=-
2+
•
∵
•
=|
||
|cos∠BAC=2，
2=|
|2=1
∴
•
-
•
=-
2+
•
=1．
故答案为：1．
| BP |
| CQ |
| AP |
| CB |
| AP |
| AB |
| AQ |
| AC |
| AP |
| AB |
| AC |
而
| AQ |
| AP |
则
| BP |
| CQ |
| AP |
| CB |
| AP |
| AB |
| AP |
| AC |
| AP |
| AB |
| AC |
| AP |
| AB |
| AC |
∵
| AB |
| AC |
| AB |
| AC |
| AP |
| AP |
∴
| BP |
| CQ |
| AP |
| CB |
| AP |
| AB |
| AC |
故答案为：1．
点评：本题主要考查向量知识在几何中的应用问题．一般在求解此类问题时，常用三角形法则或平行四边形法则把问题转化．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
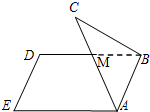如图，已知等边三角形ABC与正方形ABDE有一公共边AB，二面角C-AB-D的余弦值为