题目内容
2. 如图.已知空间四边形ABCD中,AD=BC,M,N分别为AB和CD的中点,且直线BC与MN所成的角为36°,求BC与AD所成的角.
如图.已知空间四边形ABCD中,AD=BC,M,N分别为AB和CD的中点,且直线BC与MN所成的角为36°,求BC与AD所成的角.
分析 取AC中点E,取BD中点F,连结ME、NE、NF,由已知得ME∥NF,ME=NE=NF,∠ENF是BC与AD所成的角,由此能求出BC与AD所成的角的大小.
解答 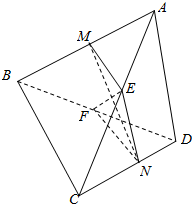 解:取AC中点E,取BD中点F,连结ME、NE、NF,
解:取AC中点E,取BD中点F,连结ME、NE、NF,
∵空间四边形ABCD中,AD=BC,M,N分别为AB和CD的中点,
∴ME∥BC,NF∥BC,NE∥AD,且ME=$\frac{1}{2}BC=NF$,NE=$\frac{1}{2}AD$,
∴ME∥NF,ME=NE=NF,
∴M、E、N、F共面,
∵直线BC与MN所成的角为36°,
∴∠EMN=∠ENM=∠MNF=36°,
∴∠ENF=∠ENM+∠MNF=72°,
∵NF∥BC,NE∥AD,
∴∠ENF是BC与AD所成的角,
∴BC与AD所成的角为72°.
点评 本题考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.已知{an}为等差数列,{bn}为等比数列,其公比q≠1且bi>0(i=1,2,…,n),若a1=b1,a11=b11,则( )
| A. | a6>b6 | B. | a6=b6 | C. | a6<b6 | D. | a6<b6或a6>b6 |
 (1)已知函数f(x)=|x-1|+|x-a|.若不等式f(x)≥a恒成立,求实数a的取值范围.
(1)已知函数f(x)=|x-1|+|x-a|.若不等式f(x)≥a恒成立,求实数a的取值范围.