题目内容
如图,在长方体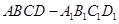 中,
中,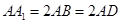 ,且
,且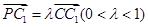 .
.
(I)求证:对任意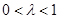 ,总有
,总有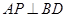 ;
;
(II)若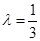 ,求二面角
,求二面角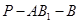 的余弦值;
的余弦值;
(III)是否存在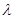 ,使得
,使得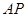 在平面
在平面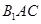 上的射影平分
上的射影平分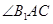 ?若存在, 求出
?若存在, 求出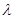 的值, 若不存在,说明理由.
的值, 若不存在,说明理由.
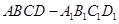 中,
中,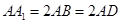 ,且
,且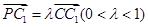 .
.
(I)求证:对任意
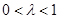 ,总有
,总有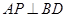 ;
;(II)若
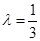 ,求二面角
,求二面角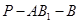 的余弦值;
的余弦值;(III)是否存在
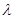 ,使得
,使得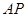 在平面
在平面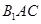 上的射影平分
上的射影平分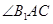 ?若存在, 求出
?若存在, 求出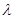 的值, 若不存在,说明理由.
的值, 若不存在,说明理由.(I)见解析(II)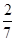 (III)存在
(III)存在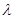
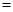
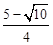
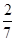 (III)存在
(III)存在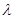
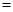
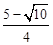
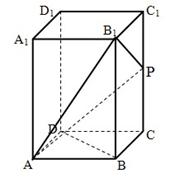
试题分析:(I)以
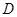 为坐标原点,分别以
为坐标原点,分别以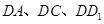 所在直线为
所在直线为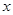 轴,
轴,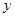 轴,
轴,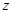 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设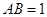 ,则
,则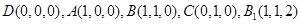 ,
,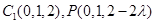 ,从而
,从而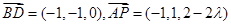 ,
,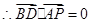 ,即
,即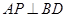 . ……4分
. ……4分(II)由(I)及
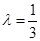 得,
得,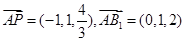 ,
,设平面
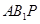 的法向量为
的法向量为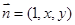 ,则
,则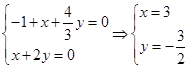 ,
,从而可取平面
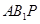 的法向量为
的法向量为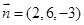 ,
,又取平面
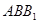 的法向量为
的法向量为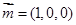 ,且设二面角
,且设二面角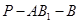 为
为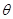 ,
,所以
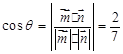 ……8分
……8分(III) 假设存在实数
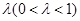 满足条件,由题结合图形,只需满足
满足条件,由题结合图形,只需满足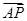 分别与
分别与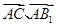 所成的角相等,
所成的角相等,即
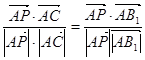 ,即
,即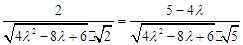 ,
,解得
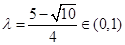 .
.所以存在满足题意得实数
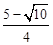 ,
,使得
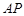 在平面
在平面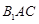 上的射影平分
上的射影平分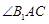 . ……12分
. ……12分点评:立体几何问题可以转化为用空间向量来解决,可以省去作二面角、线面角等步骤之间求解,但是求解时一定要注意运算的准确性.

练习册系列答案
相关题目
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 底面
底面 ,
, 是
是 的中点,作
的中点,作 交
交 于点
于点 .
.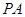 //平面
//平面 ;
; 的大小;
的大小; .
.
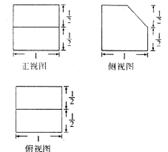

 cm3
cm3 cm3
cm3 cm3
cm3 









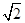 、
、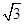 ,则此三棱锥的外接球的表面积是( )
,则此三棱锥的外接球的表面积是( )




