题目内容
【题目】如图,四棱锥P-ABCD中,AD⊥平面PAB,AP⊥AB.
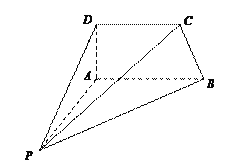
(1)求证:CD⊥AP;
(2)若CD⊥PD,求证:CD∥平面PAB;
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)由![]() 平面,得到
平面,得到![]() ,由
,由![]() ,进而证得
,进而证得![]() 平面
平面![]() ,即可证明
,即可证明![]() ;
;
(2)首先证得![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,得到
,得到![]() ,利用直线与平面平行的判定定理,即可证得结论。
,利用直线与平面平行的判定定理,即可证得结论。
试题解析:
(1)因为AD⊥平面PAB,AP平面PAB,
所以AD⊥AP.又因为AP⊥AB ,AB∩AD=A,AB平面ABCD,AD平面ABCD,
所以AP⊥平面ABCD. 因为CD平面ABCD,
所以CD⊥AP.
(2)因为CD⊥AP,CD⊥PD,且PD∩AP=P,PD平面PAD,AP平面PAD,
所以CD⊥平面PAD. ①
因为AD⊥平面PAB,AB平面PAB,
所以AB⊥AD.
又因为AP⊥AB,AP∩AD=A,AP平面PAD,AD平面PAD,
所以AB⊥平面PAD. ②
由①②得CD∥AB,
因为CD![]() 平面PAB,AB平面PAB,
平面PAB,AB平面PAB,
所以CD∥平面PAB.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
