题目内容
已知 ,且a>0,b>0,求a+b最小值。
,且a>0,b>0,求a+b最小值。
 ,且a>0,b>0,求a+b最小值。
,且a>0,b>0,求a+b最小值。9
由a>0,b>0,  . 得a+b=(a+b)×1=(a+b)×(
. 得a+b=(a+b)×1=(a+b)×(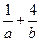 )=5+
)=5+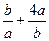 ≥5+2
≥5+2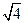 ="9. " 当且仅当
="9. " 当且仅当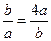 ,即b="2a," 即a=3,b=6时,(a+b)min=9.
,即b="2a," 即a=3,b=6时,(a+b)min=9.
解法二由 且a>0,b>0得(a-1)(b-4)=4,
且a>0,b>0得(a-1)(b-4)=4,
又∵0<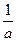 <1,0<
<1,0<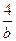 <1, ∴a>1,b>4,a-1>0,b-4>0.
<1, ∴a>1,b>4,a-1>0,b-4>0.
∴ (a-1)+(b-4) ≥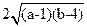 =4。 当且仅当a-1=b-4,即a=3,b=6时, (a+b)min=9.
=4。 当且仅当a-1=b-4,即a=3,b=6时, (a+b)min=9.
 . 得a+b=(a+b)×1=(a+b)×(
. 得a+b=(a+b)×1=(a+b)×(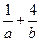 )=5+
)=5+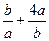 ≥5+2
≥5+2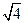 ="9. " 当且仅当
="9. " 当且仅当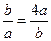 ,即b="2a," 即a=3,b=6时,(a+b)min=9.
,即b="2a," 即a=3,b=6时,(a+b)min=9.解法二由
 且a>0,b>0得(a-1)(b-4)=4,
且a>0,b>0得(a-1)(b-4)=4,又∵0<
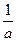 <1,0<
<1,0<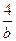 <1, ∴a>1,b>4,a-1>0,b-4>0.
<1, ∴a>1,b>4,a-1>0,b-4>0.∴ (a-1)+(b-4) ≥
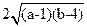 =4。 当且仅当a-1=b-4,即a=3,b=6时, (a+b)min=9.
=4。 当且仅当a-1=b-4,即a=3,b=6时, (a+b)min=9.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 、
、 、
、 ,且满足
,且满足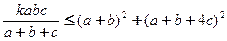 ,求
,求 的最大值。
的最大值。 ,x+y的最小值为18,
,x+y的最小值为18, ,
, ,其中a,b为常数,那么mx+ny 的最大值为
,其中a,b为常数,那么mx+ny 的最大值为 



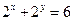 , 则
, 则 的最大值是___
的最大值是___ ,且
,且 ,则
,则 的最大值等于_____________。
的最大值等于_____________。