题目内容
已知函数 的交点的横坐标为
的交点的横坐标为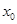 ,当
,当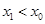 时
时
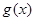 (从>,<,=,≥,≤,无法确定,中选你认为正确的一个填到横线上)
(从>,<,=,≥,≤,无法确定,中选你认为正确的一个填到横线上)
>
解析试题分析: 为减函数,
为减函数,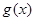 为增函数,故两函数只有1个交点,故当
为增函数,故两函数只有1个交点,故当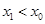 时
时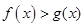 .
.
考点:函数单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知函数 的交点的横坐标为
的交点的横坐标为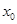 ,当
,当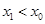 时
时
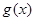 (从>,<,=,≥,≤,无法确定,中选你认为正确的一个填到横线上)
(从>,<,=,≥,≤,无法确定,中选你认为正确的一个填到横线上)
>
解析试题分析: 为减函数,
为减函数,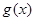 为增函数,故两函数只有1个交点,故当
为增函数,故两函数只有1个交点,故当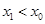 时
时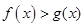 .
.
考点:函数单调性.

 阅读快车系列答案
阅读快车系列答案