题目内容
已知数列 中,
中, ,且有
,且有 .
.
(1)写出 所有可能的值;
所有可能的值;
(2)是否存在一个数列 满足:对于任意正整数
满足:对于任意正整数 ,都有
,都有 成立?若有,请写出这个数列的前6项,若没有,说明理由;
成立?若有,请写出这个数列的前6项,若没有,说明理由;
(3)求 的最小值.
的最小值.
(1)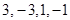 (2) 存在,
(2) 存在, 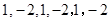 (或者取
(或者取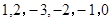 )(3)1
)(3)1
解析试题分析:
(1)根据 ,计算
,计算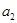 的值有两个,根据
的值有两个,根据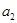 的两个值,再计算
的两个值,再计算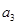 即可.
即可.
(2)罗列出所有的可能数列,从中观察是否有满足 (即
(即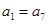 )的即可.
)的即可.
(3)根据 特点可知
特点可知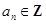 ,且所有的奇数项都为奇数,偶数项为偶数, 因此
,且所有的奇数项都为奇数,偶数项为偶数, 因此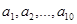 中一定有5个奇数,5个偶数,所以
中一定有5个奇数,5个偶数,所以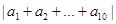 一定是奇数,所以
一定是奇数,所以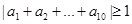 .
.
(1) 根据题意 ,且有
,且有 ,所以可得
,所以可得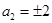 ,带入
,带入 ,可得
,可得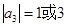
所以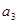 可能取的值
可能取的值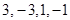
(2) 存在
这个数列的前6项可以为 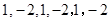 (或者取
(或者取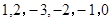 )
)
(3)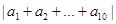 的最小值为1
的最小值为1
因为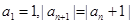 ,所以
,所以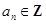 ,且所有的奇数项都为奇数,偶数项为偶数
,且所有的奇数项都为奇数,偶数项为偶数
因此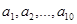 中一定有5个奇数,5个偶数,
中一定有5个奇数,5个偶数,
所以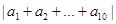 一定是奇数,所以
一定是奇数,所以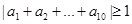
令这10项分别为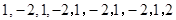
(或者为 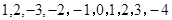 ,或者为
,或者为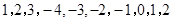 )
)
则有 .
.
考点:数列的综合应用.

练习册系列答案
相关题目
 的图象在点
的图象在点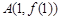 处的切线
处的切线 与直线
与直线 平行,若数列
平行,若数列 的前
的前 项和为
项和为 ,则
,则 的值为 .
的值为 . =3n-2.
=3n-2. ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m. ,且
,且 按某种顺序排列成等差数列.
按某种顺序排列成等差数列. 的值;
的值; 的首项和公差都为
的首项和公差都为 的首项和公比都为
的首项和公比都为 项和分别为
项和分别为 ,且
,且 ,求满足条件的自然数
,求满足条件的自然数 所表示的平面区域为
所表示的平面区域为 ,记
,记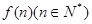
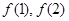 的值及
的值及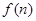 的表达式;
的表达式;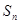 为数列
为数列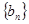 的前
的前 项的和,其中
项的和,其中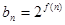 ,问是否存在正整数
,问是否存在正整数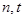 ,使
,使 成立?若存在,求出正整数
成立?若存在,求出正整数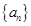 的前三项分别为
的前三项分别为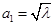 ,
, ,
,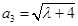 ,(其中
,(其中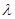 为正常数)。设
为正常数)。设
 。
。 的值;
的值;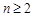 时,
时,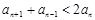 .
. =
= ,求
,求 的值;
的值;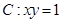 ,过
,过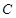 上一点
上一点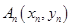 作一斜率为
作一斜率为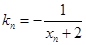 的直线交曲线
的直线交曲线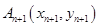 (
(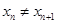 且
且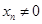 ,点列
,点列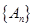 的横坐标构成数列
的横坐标构成数列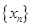 ,其中
,其中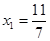 .
.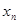 与
与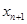 的关系式;
的关系式;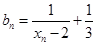 ,求证:数列
,求证:数列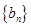 是等比数列;
是等比数列;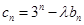 (
( 为非零整数,
为非零整数,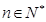 ),试确定
),试确定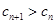 成立.
成立.