题目内容
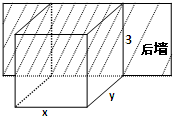
某家庭要建造一个长方体形储物间,其容积为2400m3,高为3m,后面有一面旧墙可以利用,没有花费,底部也没有花费,而长方体的上部每平方米的造价为150元,周边三面竖墙(即不包括后墙)每平方米的造价为120元,怎样设计才能使总造价最低?最低总造价是多少?


设长方体的长为xm,宽为ym,总造价为z元.
则由题意知3xy=2400,xy=800,2yx=1600.
∴z=xy×150+3(x+2y)×120=800×150+3(x+2y)×120=120000+360(x+2y)≥120000+360×2
=120000+360×2
=148800.
当且仅当
,即
时,取等号,即总造价最低.
答:当长方体的底面设计成长为40m,宽为20m的长方形时总造价最低,最低总造价是148800元.
则由题意知3xy=2400,xy=800,2yx=1600.
∴z=xy×150+3(x+2y)×120=800×150+3(x+2y)×120=120000+360(x+2y)≥120000+360×2
| x×2y |
=120000+360×2
| 1600 |
当且仅当
|
|
答:当长方体的底面设计成长为40m,宽为20m的长方形时总造价最低,最低总造价是148800元.


练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 (a为常数)所表示的平面区域的面积等于2,则实数a的值为 .
(a为常数)所表示的平面区域的面积等于2,则实数a的值为 .