题目内容
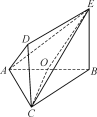
【题目】已知空间四边形ABCD，
，
，
，
，且平面
平面BCD，则该几何体的外接球的表面积为（ ）
A.
B.
C.
D.
【答案】B
【解析】
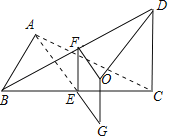
由题意画出图形，找出外接球的球心，求解三角形得到半径，代入球的表面积公式求解．
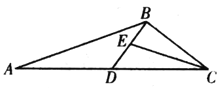
如图所示，取BC中点E，连接AE并延长至
的外心G，在中，由
，
，
可得BE＝CE＝3，则BC＝6，又
，
，满足
，则
是为以BD为斜边的直角三角形，
则BD中点F为的外心，∵平面ABC⊥平面BCD，过F作平面BCD的垂线与过G作平面ABC的垂线相交于O，
∴O为空间四边形ABCD的外接球的球心．在中，由正弦定理得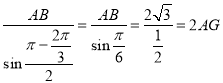
，得AG＝2
．
∴
，则OF＝，∴空间四边形ABCD的外接球的半径R＝OD＝
．
∴空间四边形ABCD的外接球的表面积
．
故选：B．
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战，某帮扶单位为帮助定点扶贫村扶贫. 此帮扶单位为了了解某地区贫困户对其所提供的帮扶的满意度，随机调查了40个贫困户，得到贫困户的满意度评分如下：
贫困户编号 | 评分 | 贫困户编号 | 评分 | 贫困户编号 | 评分 | 贫困户编号 | 评分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系统抽样法从40名贫困户中抽取容量为10的样本，且在第一分段里随机抽到的评分数据为92.
（1）请你列出抽到的10个样本的评分数据；
（2）计算所抽到的10个样本的均值
和方差
；
（3）在（2）条件下，若贫困户的满意度评分在
之间，则满意度等级为“
级”.运用样本估计总体的思想，现从（1）中抽到的10个样本的满意度为“
级”贫困户中随机地抽取2户，求所抽到2户的满意度均评分均“超过80”的概率.
（参考数据：
）
