题目内容
【题目】已知直线l的方程为x=﹣2,且直线l与x轴交于点M,圆O:![]() 与x轴交于A,B两点(如图).
与x轴交于A,B两点(如图).
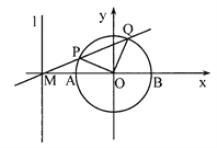
(1)过M点的直线l1交圆于P、Q两点,且O点到直线l1的距离为![]() ,求直线l1的方程;
,求直线l1的方程;
(2)求以l为准线,中心在原点,且短轴长为圆O的半径的椭圆方程;
(3)过M点的圆的切线l2,交(2)中的一个椭圆于C、D两点,其中C、D两点在x轴上方,求线段CD的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)可设直线l1的方程为y=k(x+2),由点到直线的距离公式可得k的方程,解方程可得;
(2)设椭圆的方程为![]() 1(a>b>0),易得a=1或b=1,分别可得b和a值,可得方程;
1(a>b>0),易得a=1或b=1,分别可得b和a值,可得方程;
(3)可设直线l2的方程为y![]() (x+2)和椭圆联立可得5x2+8x+2=0,由弦长公式可得.
(x+2)和椭圆联立可得5x2+8x+2=0,由弦长公式可得.
(1)∵![]() 点到直线
点到直线![]() 的距离为
的距离为![]() .
.
设![]() 的方程为
的方程为![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() 的方程为
的方程为![]() .
.
(2)设椭圆方程为![]() ,半焦距为
,半焦距为![]() ,则
,则![]() .
.
![]() ,
,![]() ,∴
,∴![]() .∴所求椭圆方程为
.∴所求椭圆方程为![]() .
.
(3)设切点为![]() ,则由题意得,椭圆方程为
,则由题意得,椭圆方程为![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,则
,则![]() ,
,
∴![]() 的方程为
的方程为![]() ,代入椭圆
,代入椭圆![]() 中,整理得
中,整理得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求y关于x的线性回归方程.
(3)如果广告费支出为一千万元,预测销售额大约为多少百万元?
参考公式用最小二乘法求线性回归方程系数公式: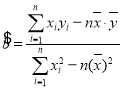 ,
,![]() .
.