题目内容
8．已知等比数列{an}为递增数列，a1=-2，且2（an+an+2）=5an+1，则公比q=$\frac{1}{2}$．．分析 由数列{an}为等比数列，a1=-2，且2（an+an+2）=5an+1，利用等比数列的通项公式可得：$2（{a}_{n}+{a}_{n}{q}^{2}）=5{a}_{n}q$，解出q，再利用等比数列{an}为递增数列，即可得出．
解答 解：∵数列{an}为等比数列，a1=-2，且2（an+an+2）=5an+1，
∴$2（{a}_{n}+{a}_{n}{q}^{2}）=5{a}_{n}q$，
化为2q2-5q+2=0，
解得q=$\frac{1}{2}$或2．
又等比数列{an}为递增数列，
∴取q=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查了等比数列的通项公式、单调性，考查了推理能力与计算能力，属于基础题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
18．
已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，为得到g（x）=cosωx的图象，则只要将f（x）的图象（ ）
已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，为得到g（x）=cosωx的图象，则只要将f（x）的图象（ ）| A． | 向右平移$\frac{π}{6}$个单位长度 | B． | 向左平移$\frac{π}{12}$个单位长度 | ||
| C． | 向左平移$\frac{π}{6}$个单位长度 | D． | 向右平移$\frac{π}{12}$个单位长度 |
19．设直线x-3y+m=0（m≠0）与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两条渐近线分别交于点A，B，若点P（m，0）满足|PA|=|PB|，则该双曲线的离心率是（ ）
| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{5}{2}$ | D． | $\sqrt{5}$+1 |
16．在《爸爸去哪儿》第二季第四期中，假如村长给6位“萌娃”布置一项到A、B、C三个位置搜寻空投食物的任务，每两位“萌娃”搜寻一个位置．考虑到位置远近及年龄大小，Grace不去较远的A位置，多多不去较近的C位置，则不同的搜寻安排方案有（ ）
| A． | 20 种 | B． | 40 种 | C． | 42种 | D． | 48种 |
若如图为某直三棱柱（侧棱与底面垂直）被削去一部分后的直观图与三视图中的侧视图、俯视图，则其正视图的面积为4，三棱锥D-BCE的体积为$\frac{8}{3}$．
13．某正三棱柱的三视图如图所示，其中正（主）视图是正方形，该正三棱柱的侧视图的面积是（ ）
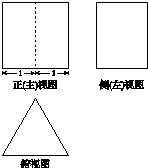
| A． | 2$\sqrt{3}$ | B． | 4 | C． | $\sqrt{3}$ | D． | 2 |
16．已知a，b∈R，则“ab=4”是“直线2x+ay-1=0与bx+2y+1=0平行”的（ ）
| A． | 充分必要条件 | B． | 充分而不必要条件 | ||
| C． | 必要而不充分条件 | D． | 既不充分也不必要条件 |
