题目内容
【题目】(2017·金华调研)如图,AB=BE=BC=2AD=2,且AB⊥BE,∠DAB=60°,AD∥BC,BE⊥AD.
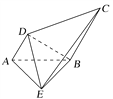
(1)求证:平面ADE⊥平面BDE;
(2)求直线AD与平面DCE所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先根据平几知识得AD⊥DB ,又BE⊥AD,得AD⊥平面BDE ,根据面面垂直判定定理得结论,(2)先根据等体积法V A-DCE=V E-ADC可得点A到平面DCE的距离,根据线面角定义得直线AD与平面DCE所成角的正弦值.
试题解析:(1)证明 ∵AB=2AD,∠DAB=60°,∴AD⊥DB,
又BE⊥AD,且BD∩BE=B,∴AD⊥平面BDE,
又AD平面ADE,∴平面ADE⊥平面BDE.
(2)解 ∵BE⊥AD,AB⊥BE,∴BE⊥平面ABCD,
∴点E到平面ABCD的距离就是线段BE的长为2,
设AD与平面DCE所成角为θ,点A到平面DCE的距离为d,
由V三棱锥A-DCE=V三棱锥E-ADC得![]() ×d×S△CDE=
×d×S△CDE=![]() ×|BE|×S△ACD,解得d=
×|BE|×S△ACD,解得d=![]() ,
,
而AD=1,则sin θ=![]() =
=![]() ,
,
故直线AD与平面DCE所成角的正弦值为![]() .
.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目