题目内容
幂函数
，其中
，且在
上是减函数，又
，则
=（ ）
| A．0 | B．1 | C．2 | D．3 |
B
解析试题分析：由题意知
，解得
，由知函数
为偶函数，又因，所以
，故选B．
考点：1．幂函数的解析式样 2．幂函数的单调性与奇偶性．
练习册系列答案
相关题目
函数
的零点所在的区间是（ ）
A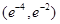． | B． | C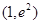． | D． |
规定
表示不超过
的最大整数，
，若方程
有且仅有四个实数根，则实数
的取值范围是（ ）
A． | B． | C． | D． |
已知
，若对任意
与
的值至少有一个为正数，则实数
的取值范围是（ ）
A． | B． | C． | D． |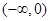
函数
（ ）
A． | B． |
C． | D． |
如果偶函数
在
上是增函数且最小值是2，那么在
上是（ ）
A．减函数且最小值是 | B．减函数且最大值是 |
| C．增函数且最小值是 | D．增函数且最大值是 |
己知函数f(x)=
在[-1，1]上的最大值为M(a)，则函数g(x)=M(x)-
的零点个数为
| A．1个 | B．2个 | C．3个 | D．4个 |
若
是奇函数，且在
内是增函数，又
，则
的解集是（ ）
A． ； | B． |
C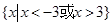． ； | D． |