题目内容
函数
的零点所在的区间是（ ）
A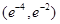． | B． | C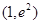． | D． |
B
解析试题分析：根据对数函数的性质可知为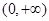
的单调递增函数，所以该函数的零点要么只有一个，要么没有，而
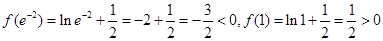，根据零点存在定理可知
在有唯一零点，故选B.
考点：1.函数的单调性；2.函数的零点.
练习册系列答案
相关题目
函数
的零点所在的区间是（ ）
A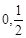．( ) | B．( ) | C．( ) | D．( ) |
下列函数在区间
是增函数的是
A． | B． | C． | D． |
下列函数中，既是奇函数又是增函数的为（ ）
A． | B． | C． | D． |
已知函数
，若关于
的方程
有两个不同的实根，则实数
的取值范围是（ ）
A． | B． | C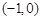． | D． |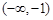
在区间
上不是增函数的是（ ）
A． | B． | C． | D． |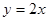
已知偶函数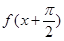
,当
时，
,设
，则( )
A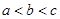． | B． | C． | D． |
幂函数
，其中
，且在
上是减函数，又
，则
=（ ）
| A．0 | B．1 | C．2 | D．3 |
定义在R上的奇函数f(x)，当x≥0时，f(x)＝
则关于x的函数F(x)＝f(x)－a(0<a<1)的所有零点之和为( )．
| A．1－2a | B．2a－1 |
| C．1－2－a | D．2－a－1 |