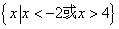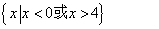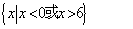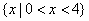题目内容
设函数 ,
, . 若当
. 若当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数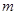 的取值范围是( ).
的取值范围是( ).
 ,
, . 若当
. 若当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数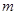 的取值范围是( ).
的取值范围是( ).A. | B.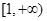 | C. | D. |
A
试题分析:∵
 。
。设
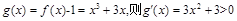 ,
,所以g(x)是递增的奇函数。
由f(msinθ)+f(1-m)>2,
∴f(msinθ)-1>1-f(1-m),即g(msinθ)>g(m-1)
∴msinθ>m-1,∴1>m(1-sinθ)。
因为0<θ<
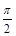 时,
时,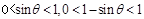 ,
,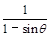 >1,而m<
>1,而m<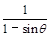 ,
,∴m
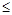 1.故选A。
1.故选A。点评:中档题,抽象不等式问题,武威要利用函数的奇偶性、单调性,转化成具体不等式。恒成立问题,往往要通过“分离参数法”转化成求函数的最值问题。本题比较典型。

练习册系列答案
相关题目
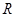 上的奇函数
上的奇函数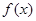 满足
满足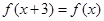 ,当
,当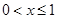 时,
时,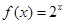 ,则
,则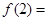 ( )
( )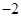
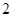
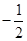
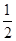
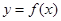 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当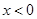 时,
时,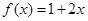 ,则当
,则当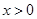 时,
时, 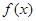 = .
= .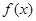 是R上的单调增函数且为奇函数,数列
是R上的单调增函数且为奇函数,数列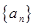 是等差数列,
是等差数列,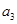 >0,则
>0,则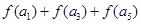 的值 ( )
的值 ( )
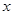 ,有
,有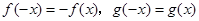 ,且
,且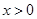 时
时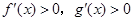 ,则
,则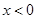 时( )
时( )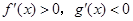
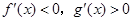

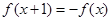 ,若
,若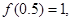 则
则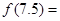 ________;
________;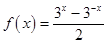 是( )
是( )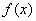 满足
满足
 ,则
,则 ( )
( )