Question

已知数列{a_n}满足a₁=a，a₂=2，S_n是数列的前n项和，且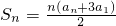（n∈N*）．
（1）求实数a的值；
（2）求数列{a_n}的通项公式；
（3）对于数列{b_n}，若存在常数M，使b_n＜M（n∈N*），且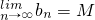，则M叫做数列{b_n}的“上渐近值”．设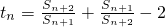（n∈N*），T_n为数列{t_n}的前n项和，求数列{T_n}的上渐近值．

Answer 1

解：（1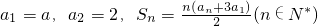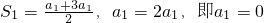）∵，∴．（2分）∴a=0．

（2）由（1）可知，．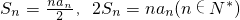
∴2S_n-1=（n-1）a_n-1（n≥2）．
∴2（S_n-S_n-1）=na_n-（n-1）a_n-1，2a_n=na_n-（n-1）a_n-1，（n-2）a_n=（n-1）a_n-1．
∴．
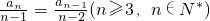因此，．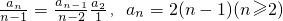
又a₁=0，∴数列{a_n}的通项公式a_n=2（n-1）（n∈N^*）．
（3）由（2）有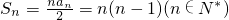，．于是，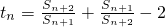
=
=．
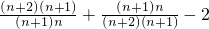
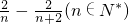∴T_n=t₁+t₂+…+t_n
=
=．
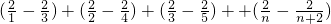
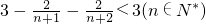又，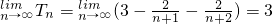
∴数列{T_n}的上渐近值是3．

分析：（1）由题设条件可知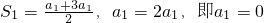．由此能够解得a=0．
（2）由题意可知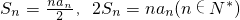，．所以2S_n-1=（n-1）a_n-1（n≥2）．由此可知数列{a_n}的通项公式a_n=2（n-1）（n∈N^*）．
（3）由题设条件知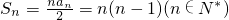．由此可知T_n=t₁+t₂+…+t_n=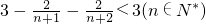．从而求得数列{T_n}的上渐近值是3．
点评：本题考查数列的综合运用，解题时要注意计算能力的培养．