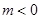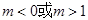题目内容
已知△ABC外接圆半径R＝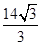
，且∠ABC＝120°，BC＝10，边BC在x轴上且y轴垂直平分BC边，则过点A且以B、C为焦点的双曲线方程为______________．
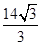，且∠ABC＝120°，BC＝10，边BC在x轴上且y轴垂直平分BC边，则过点A且以B、C为焦点的双曲线方程为______________．
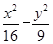＝1∵sin∠BAC＝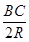
＝
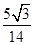，∴cos∠BAC＝
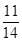，AC＝2Rsin∠ABC＝2××
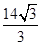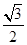＝14，
sin∠ACB＝sin(60°－∠BAC)＝sin60°cos∠BAC－cos60°·sin∠BAC＝
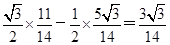，∴AB＝2Rsin∠ACB＝2×
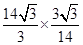＝6,
∴2a＝|AC－AB|＝14－6＝8，
∴a＝4，又c＝5，∴b2＝c2－a2＝25－16＝9，∴所求双曲线方程为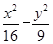＝1.
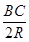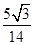＝，∴cos∠BAC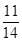＝，AC＝2Rsin∠ABC＝2×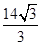×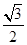＝14，sin∠ACB＝sin(60°－∠BAC)＝sin60°cos∠BAC－cos60°·sin∠BAC＝
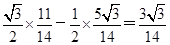，∴AB＝2Rsin∠ACB＝2×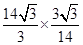＝6,∴2a＝|AC－AB|＝14－6＝8，
∴a＝4，又c＝5，∴b2＝c2－a2＝25－16＝9，∴所求双曲线方程为
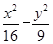＝1.
练习册系列答案
名校课堂系列答案
相关题目
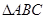的内切圆与三边
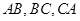的切点分别为
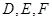,已知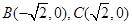
，内切圆圆心
,设点A的轨迹为R.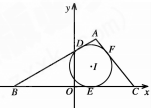 
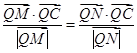恒成立，若求出Q点的坐标，若不存在，说明理由.
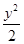＝1，过定点P(2，1)作直线交双曲线于P1、P2两点，并使P(2，1)为P1P2的中点，则此直线方程是____________．
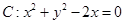的圆心到双曲线
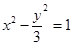的渐近线的距离是（ ）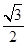
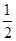
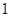
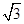
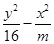＝1的离心率e＝2，则m＝________．
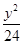＝1的两个焦点，P是双曲线上的一点，且3PF1＝4PF2，则△PF1F2的面积等于________．
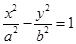的右焦点，双曲线两渐近线分另。为l1，l2过F作直线l1的垂线，分别交l1，l2于A，B两点．若OA, AB, OB成等差数列，且向量
与
同向，则双曲线的离心率e的大小为( )
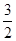
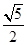
,则双曲线C1:
-
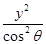=1与C2:
(
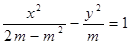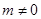），若双曲线的离心率
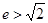，则实数m的取值范围是（ ）
