题目内容
定义在R上的函数f(x)即是偶函数又是周期函数,若f(x)的最小正周期是π,且当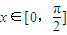 时,f(x)=sinx,则
时,f(x)=sinx,则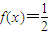 的解为( )
的解为( )A.
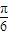
B.
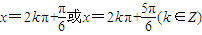
C.
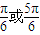
D.
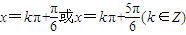
【答案】分析:先根据偶函数性质求出f(x)在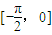 上的解析式,再求出在一个最小正周期
上的解析式,再求出在一个最小正周期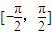 内的解,最后根据周期性求出所有的解.
内的解,最后根据周期性求出所有的解.
解答:解:当 时,f(x)=sinx,当
时,f(x)=sinx,当 时,
时,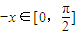 ,∵函数f(x)是偶函数,∴f(x)=f(-x)=sin(-x)=-sinx.
,∵函数f(x)是偶函数,∴f(x)=f(-x)=sin(-x)=-sinx.
在一个周期 内,
内,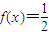 的解分别由sinx=
的解分别由sinx= ,解得x=
,解得x=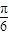 ,由sinx=-
,由sinx=- ,解得x=-
,解得x=-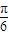 .函数f(x)又是周期函数,若最小正周期是π,
.函数f(x)又是周期函数,若最小正周期是π,
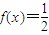 的解为x=kπ±
的解为x=kπ± ,k∈Z,即
,k∈Z,即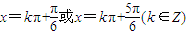 .
.
故选D
点评:本题考查三角方程求解,函数的周期性和奇偶性.考查逻辑思维能力、计算能力.
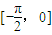 上的解析式,再求出在一个最小正周期
上的解析式,再求出在一个最小正周期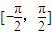 内的解,最后根据周期性求出所有的解.
内的解,最后根据周期性求出所有的解.解答:解:当
 时,f(x)=sinx,当
时,f(x)=sinx,当 时,
时,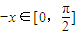 ,∵函数f(x)是偶函数,∴f(x)=f(-x)=sin(-x)=-sinx.
,∵函数f(x)是偶函数,∴f(x)=f(-x)=sin(-x)=-sinx.在一个周期
 内,
内,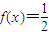 的解分别由sinx=
的解分别由sinx= ,解得x=
,解得x=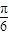 ,由sinx=-
,由sinx=- ,解得x=-
,解得x=-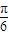 .函数f(x)又是周期函数,若最小正周期是π,
.函数f(x)又是周期函数,若最小正周期是π,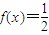 的解为x=kπ±
的解为x=kπ± ,k∈Z,即
,k∈Z,即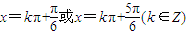 .
.故选D
点评:本题考查三角方程求解,函数的周期性和奇偶性.考查逻辑思维能力、计算能力.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目