题目内容
已知数列 满足:
满足: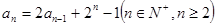 且
且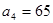 .(1)求数列
.(1)求数列 的前三项;(2)是否存在一个实数
的前三项;(2)是否存在一个实数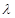 ,使数列
,使数列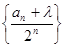 为等差数列?若存在,求出
为等差数列?若存在,求出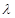 的值;若不存在,说明理由;(3)求数列
的值;若不存在,说明理由;(3)求数列 的前
的前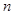 项和
项和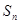 .
.
(1)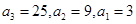 (2)
(2)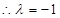 时,
时,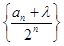 成等差数列
成等差数列
(3)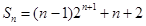
解析试题分析:本题第(1)问,直接根据条件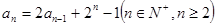 ,取n=1,2,3,代入即可求解;
,取n=1,2,3,代入即可求解;
第(2)问,先假设其存在,然后根据等差数列对应的相邻两项的差为常数即可求出λ的值;
第(3)问,先根据条件求出数列{an}的通项公式,再借助于分组求和以及错位相减求和即可求出结论.
解:(1)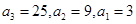
(2)
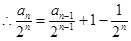 ,
,

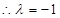 时,
时,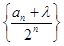 成等差数列
成等差数列
(3) 
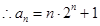

令 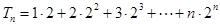
则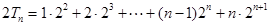
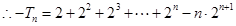
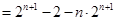
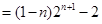
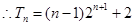
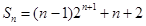
考点:数列递推式;等差关系的确定;数列的求和.
点评:本题主要考察利用数列的递推式求数列的特定项以及数列的求和问题.本题涉及到数列求和的分组法以及错位相减法,错位相减法适用于一等差数列与一等比数列相乘组成的新数列.

练习册系列答案
相关题目
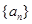 的前
的前 项和为
项和为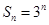 ,数列
,数列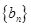 满足
满足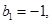
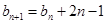 (
(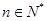 ).
).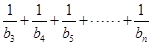 的值.
的值.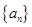 中,
中,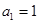 ,前
,前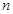 项的和是
项的和是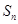 ,且
,且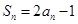 ,
,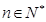 .
.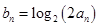 ,求
,求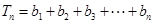 .
.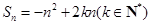 ,且
,且 的最大值为4.
的最大值为4.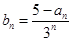 ,数列{bn}的前n项和为Tn,试比较Tn与
,数列{bn}的前n项和为Tn,试比较Tn与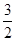 的大小.
的大小. 满足
满足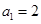 ,
,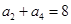 ,且对任意
,且对任意 ,函数
,函数 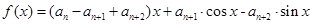 满足
满足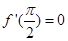
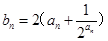 ,求数列
,求数列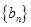 的前
的前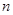 项和
项和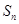 .
. 中,
中, ,
,
 且
且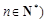 .
. ,
,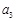 的值;
的值; 是等比数列,并求
是等比数列,并求 项和
项和 .
. 的前
的前 项和为
项和为 ,且
,且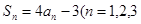 …);
…);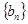 满足
满足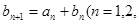 …),
…),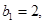 求数列
求数列 中,
中, ,
, ,
,
 为首项的等比数列,求数列
为首项的等比数列,求数列 的前m项和
的前m项和
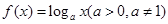 ,已知数列
,已知数列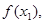
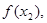
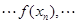 是公差为2的等差数列,且
是公差为2的等差数列,且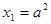 .
.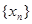 的通项公式;
的通项公式;  时,求数列
时,求数列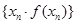 的前
的前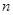 项和
项和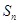 .
.