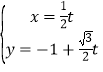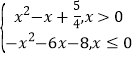题目内容
【题目】已知正方体有8个不同顶点,现任意选择其中4个不同顶点,然后将它们两两相连,可组成平面图形成空间几何体.在组成的空间几何体中,可以是下列空间几何体中的________.(写出所有正确结论的编号)
①每个面都是直角三角形的四面体;
②每个面都是等边三角形的四面体;
③每个面都是全等的直角三角形的四面体;
④有三个面为等腰直角三角形,有一个面为等边三角形的四面体.
【答案】①②④
【解析】
画出正方体的图形,在几何体中找出满足结论的图形即可.
解:
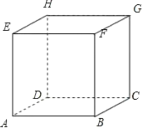
①每个面都是直角三角形的四面体;如:EABC,所以①正确;
②每个面都是等边三角形的四面体;如EBGD,所以②正确;
③每个面都是全等的直角三角形的四面体:这是不可能的,③错误;
④有三个面为等腰直角三角形,有一个面为等边三角形的四面体.如:ABDE,所以④正确;
故答案为:①②④.

练习册系列答案
相关题目