题目内容
4．如果实数x，y满足条件$\left\{\begin{array}{l}{x+y-2≥0}\\{x-1≤0}\\{y-2≤0}\end{array}\right.$，则z=$\frac{y}{x+1}$的最小值为$\frac{1}{2}$．分析 由题意作平面区域，易知z=$\frac{y}{x+1}$的几何意义是点B（x，y）与点A（-1，0）连线的直线的斜率，从而解得．
解答 解：由题意作平面区域如下，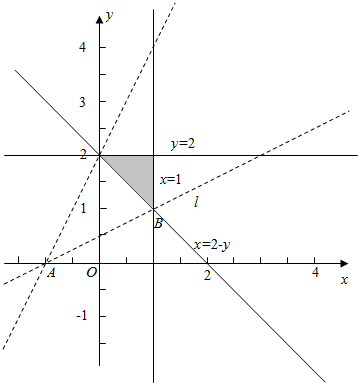
z=$\frac{y}{x+1}$的几何意义是点B（x，y）与点A（-1，0）连线的直线的斜率，
故当B（1，1）时，z=$\frac{y}{x+1}$有最小值，
z=$\frac{1}{1+1}$=$\frac{1}{2}$；
故答案为：$\frac{1}{2}$．
点评 本题考查了平面向量的应用及数形结合的思想应用，同时考查了斜率公式的应用．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
15．函数f（x）=$\sqrt{lo{g}_{\frac{1}{2}}（x-2）}$的定义域为（ ）
| A． | （2，+∞） | B． | [2，+∞） | C． | （2，3] | D． | （-∞，3] |
19．若x∈[$\frac{π}{6}，\frac{π}{3}$]，则f（x）=$\frac{\sqrt{3}cosxsin（x-\frac{π}{6}）}{sin2x}$的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | 1 | D． | $\frac{3}{2}$ |
13．函数y=$\sqrt{lo{g}_{{\;}_{\frac{1}{3}}tanx}}$的定义域是（ ）
| A． | （0，$\frac{π}{4}$] | B． | （2kπ，2kπ+$\frac{π}{4}$]，k∈Z | C． | （kπ，kπ+$\frac{π}{4}$]，k∈Z | D． | （kπ-$\frac{π}{2}$，kπ+$\frac{π}{4}$]，k∈Z |